 por Maria Tamires » Qui Jul 11, 2013 10:17
por Maria Tamires » Qui Jul 11, 2013 10:17
Estou com muita dificuldade para resolver esse exercício
Se
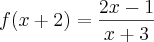
,
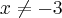
, o domínio de f(x) é:
a) R
b) R*
c) {
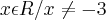
d)
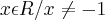
e)

Resolução
g(x)=x+2 -> f(y) -> y=x+2
![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)
Parei aí... não consigo terminar pois não sei como acha a restrição para o numerador! Me ajude por favor...
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por timoteo » Qui Jul 11, 2013 12:12
por timoteo » Qui Jul 11, 2013 12:12
Olá Tamires.
A questão pede o domínio de f(x) e este é igual a imagem de g(x). Sabendo disso qual é a imagem de g(x)?
Resposta: Im g(x) = R.
Estimas!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Maria Tamires » Qui Jul 11, 2013 13:15
por Maria Tamires » Qui Jul 11, 2013 13:15
poxa eu também pensei assim... só que meu prof falo que é a alternativa d!!
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por timoteo » Qui Jul 11, 2013 14:14
por timoteo » Qui Jul 11, 2013 14:14
Esqueci de colocar que temos que levar a condição de existência de f(x) em consideração, então com f(x) =

, a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.
Caso você tenha a resposta dele você posta ai!
Estimas!
P.S. Vamos ver se alguém tem outra opinião.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Maria Tamires » Qui Jul 11, 2013 14:32
por Maria Tamires » Qui Jul 11, 2013 14:32
Obrigada
Quando ele posta a resolução imediatamente posto aqui!
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
 por Maria Tamires » Sex Jul 12, 2013 11:56
por Maria Tamires » Sex Jul 12, 2013 11:56
Consegui chegar no resultado
realmente é a alternativa D
-
Maria Tamires
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 11, 2013 09:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3°
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2229 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5442 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4196 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17026 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3968 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
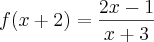 ,
, 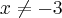 , o domínio de f(x) é:
, o domínio de f(x) é: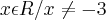
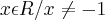

![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)

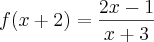 ,
, 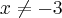 , o domínio de f(x) é:
, o domínio de f(x) é: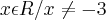
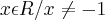

![f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5} f\left[g(x) \right]=\frac{2x-1}{x+3} => \frac{2y-1}{y+3} =>\frac{2(x+2)-1}{x+2+3} => \frac{2x+4-1}{x+5} => \frac{2x+3}{x+5}](/latexrender/pictures/c2cf91149454a9be572e5453ffbde51b.png)



 , a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.
, a condição pede x =/= -3. Portando na minha opinião a letra correta é a C.




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.