 por teilom » Dom Jul 07, 2013 12:11
por teilom » Dom Jul 07, 2013 12:11
Resolva as equações do primeiro grau, sendo u=z
A)x+1=2x-6
b)5x-6=8x+15
C)2.(x+1)-3.(x+2)=7
d)x-2.(x-3)=3.(x+8)
-
teilom
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Sáb Ago 11, 2012 20:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Leticia_alves » Dom Jul 07, 2013 18:14
por Leticia_alves » Dom Jul 07, 2013 18:14
Bom, temos que:
A)x+1=2x-6

2x - x = 1 + 6

x = 7 .
b)5x-6=8x+15

5x - 8x = 15 + 6

-3x = 21

x = -7 .
C)2.(x+1)-3.(x+2)=7

2x + 2 -3x - 6 = 7

-x = 7 - 2 + 6

-x = 11

x = -11 .
d)x-2.(x-3)=3.(x+8)

x - 2x + 6 = 3x + 24

x - 2x - 3x = 24 - 6

- 4x = 18

x = -
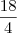

x = -

.
Bom, acho que é isso! Mas refaça cada equação e preste atenção às operações!
-
Leticia_alves
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Jun 14, 2013 19:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Juros] Não acho o tempo, não sei se estou fazendo certo
por AlexandreLuna » Ter Abr 24, 2012 20:46
- 3 Respostas
- 2931 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:10
Matemática Financeira
-
- estou com uma duvida me ajudem ai!!
por weverton » Seg Jul 12, 2010 17:54
- 2 Respostas
- 2085 Exibições
- Última mensagem por weverton

Ter Jul 13, 2010 16:50
Estatística
-
- me ajudem estou com uma duvida
 por weverton » Qua Jul 28, 2010 17:59
por weverton » Qua Jul 28, 2010 17:59
- 1 Respostas
- 3686 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 29, 2010 07:44
Estatística
-
- estou com uma duvida me ajudem ai!!
por weverton » Qua Ago 04, 2010 17:05
- 2 Respostas
- 2262 Exibições
- Última mensagem por DanielRJ

Sex Ago 20, 2010 21:15
Estatística
-
- me ajudem estou desesperada
 por Raquel Rangel » Ter Fev 15, 2011 22:28
por Raquel Rangel » Ter Fev 15, 2011 22:28
- 7 Respostas
- 6747 Exibições
- Última mensagem por Renato_RJ

Qua Fev 16, 2011 11:17
Dúvidas Pendentes (aguardando novos colaboradores)
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 2x - x = 1 + 6
2x - x = 1 + 6  x = 7 .
x = 7 . 5x - 8x = 15 + 6
5x - 8x = 15 + 6  -3x = 21
-3x = 21  x = -7 .
x = -7 . 2x + 2 -3x - 6 = 7
2x + 2 -3x - 6 = 7  -x = 7 - 2 + 6
-x = 7 - 2 + 6  -x = 11
-x = 11  x = -11 .
x = -11 . x - 2x + 6 = 3x + 24
x - 2x + 6 = 3x + 24  x - 2x - 3x = 24 - 6
x - 2x - 3x = 24 - 6  - 4x = 18
- 4x = 18  x = -
x = - 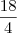
 x = -
x = -  .
.

 .
.



