Man Utd escreveu:é certo afirmar que as raízes de uma função modular se tornam bicos(pontos que não tem derivada),já que o gráfico é rebatido para cima?
Nem sempre é correto afirmar isso.
Por exemplo, x = 0 é uma raiz da função definida por

, entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.
- figura1.png (8.93 KiB) Exibido 7638 vezes
Errado. Na função definida por
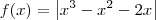
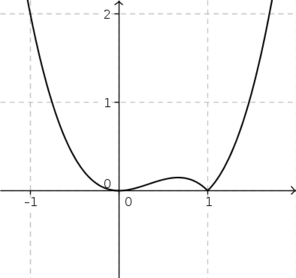
temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):
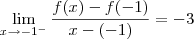


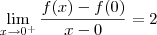
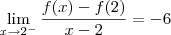
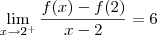
Veja também o gráfico desta função representado abaixo.

- figura2.png (11.88 KiB) Exibido 7638 vezes
Man Utd escreveu:Dúvida:eu tenho que fazer o gráfico para descobrir os possíveis bicos? ou existe um jeito mais eficaz?
Você pode calcular a derivada da função e analisar onde ela é descontínua. Entretanto, dependendo do caso é mais simples construir logo o gráfico.
Man Utd escreveu:eu tenho um exercicio assim:
Construa uma função f: R-R que seja contínua em R e derivavél em todos os pontos exceto em -1,0 e 1.
a resolução apresentada a mim foi:
(x+1).x.(x-1)----decomposição de polinomios.
x^{3}-x, então foi colocado em módulo------|x^{3}-x|,com isso as raízes apresentaram bicos na função(conforme wolfram na 1° postagem).
dúvida:Isso sempre é válido?digo uma função em módulo não vai ter derivada nos pontos que são as raízes?
att,
Nem sempre isso é válido, como ilustra o exemplo exibido no início deste texto.


![f(x) = \sqrt[3]{x} f(x) = \sqrt[3]{x}](/latexrender/pictures/ac64ffeed293f17398e36ce96a633821.png) não é derivável em x= 0 , o limite das retas tangente a função neste ponto é o próprio
não é derivável em x= 0 , o limite das retas tangente a função neste ponto é o próprio  , o coeficiente angular desta reta vai
, o coeficiente angular desta reta vai  quado
quado  .
.
 , entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.
, entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.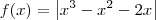 temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):
temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):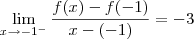


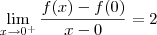
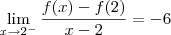
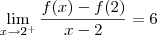



 , avisa que eu resolvo.
, avisa que eu resolvo.

