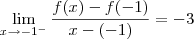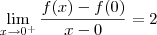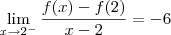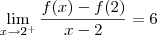por Man Utd » Sáb Jun 15, 2013 11:03
por Man Utd » Sáb Jun 15, 2013 11:03
é certo afirmar que as raízes de uma função modular se tornam bicos(pontos que não tem derivada),já que o gráfico é rebatido para cima?
nesta função |x^{3}-x| (vide o gráfico:
http://www.wolframalpha.com/input/?i=ab ... 83%29-x%29 todas as raízes encontram-se bicos).
mais nesta outra função |x^{3}-x^{2}-2x|(gráfico:
http://www.wolframalpha.com/input/?i=ab ... 2%29-2x%29 )não acontecem com todas as raízes e somente uma.
Dúvida:eu tenho que fazer o gráfico para descobrir os possíveis bicos?ou existe um jeito mais eficaz?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sáb Jun 15, 2013 13:24
por e8group » Sáb Jun 15, 2013 13:24
Man Utd escreveu:é certo afirmar que as raízes de uma função modular se tornam bicos(pontos que não tem derivada),já que o gráfico é rebatido para cima?
nesta função |x^{3}-x| (vide o gráfico:
http://www.wolframalpha.com/input/?i=ab ... 83%29-x%29 todas as raízes encontram-se bicos).
A função não é diferenciável nestes pontos ,segue de imediato da definição ,pois as derivadas laterias diferem .
SIm , em uma destas raízes ,as derivadas laterias são iguais o que implica a função diferenciável neste ponto .
Man Utd escreveu:Dúvida:eu tenho que fazer o gráfico para descobrir os possíveis bicos?ou existe um jeito mais eficaz?
Tome cuidado ,esta analise leva você dizer que as funções cujo gráfico não apresenta "bicos " é diferenciável ,isto não é verdade , por exemplo ,
![f(x) = \sqrt[3]{x} f(x) = \sqrt[3]{x}](/latexrender/pictures/ac64ffeed293f17398e36ce96a633821.png)
não é derivável em x= 0 , o limite das retas tangente a função neste ponto é o próprio

, o coeficiente angular desta reta vai

quado

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Sáb Jun 15, 2013 20:10
por Man Utd » Sáb Jun 15, 2013 20:10
eu tenho um exercicio assim:
Construa uma função f: R-R que seja contínua em R e derivavél em todos os pontos exceto em -1,0 e 1.
a resolução apresentada a mim foi:
(x+1).x.(x-1)----decomposição de polinomios.
x^{3}-x, então foi colocado em módulo------|x^{3}-x|,com isso as raízes apresentaram bicos na função(conforme wolfram na 1° postagem).
dúvida:Isso sempre é válido?digo uma função em módulo não vai ter derivada nos pontos que são as raízes?
att,
obrigado pela atenção.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Sáb Jun 15, 2013 21:26
por e8group » Sáb Jun 15, 2013 21:26
Você também pode pensar em 3 funções contínuas em toda a reta satisfazendo a (*) diferenciabilidade em todos os pontos exceto -1,0,1 . Logo , a soma destas funções contínuas fornecerá uma função contínua satisfazendo (*) .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Dom Jun 16, 2013 10:25
por Man Utd » Dom Jun 16, 2013 10:25
vlw santhiago.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por LuizAquino » Dom Jun 16, 2013 11:24
por LuizAquino » Dom Jun 16, 2013 11:24
Man Utd escreveu:é certo afirmar que as raízes de uma função modular se tornam bicos(pontos que não tem derivada),já que o gráfico é rebatido para cima?
Nem sempre é correto afirmar isso.
Por exemplo, x = 0 é uma raiz da função definida por

, entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.
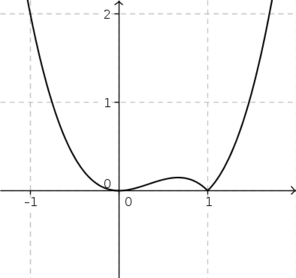
- figura1.png (8.93 KiB) Exibido 7637 vezes
Errado. Na função definida por
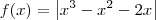
temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):
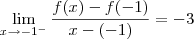


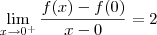
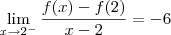
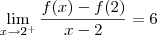
Veja também o gráfico desta função representado abaixo.

- figura2.png (11.88 KiB) Exibido 7637 vezes
Man Utd escreveu:Dúvida:eu tenho que fazer o gráfico para descobrir os possíveis bicos? ou existe um jeito mais eficaz?
Você pode calcular a derivada da função e analisar onde ela é descontínua. Entretanto, dependendo do caso é mais simples construir logo o gráfico.
Man Utd escreveu:eu tenho um exercicio assim:
Construa uma função f: R-R que seja contínua em R e derivavél em todos os pontos exceto em -1,0 e 1.
a resolução apresentada a mim foi:
(x+1).x.(x-1)----decomposição de polinomios.
x^{3}-x, então foi colocado em módulo------|x^{3}-x|,com isso as raízes apresentaram bicos na função(conforme wolfram na 1° postagem).
dúvida:Isso sempre é válido?digo uma função em módulo não vai ter derivada nos pontos que são as raízes?
att,
Nem sempre isso é válido, como ilustra o exemplo exibido no início deste texto.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada de uma função modular
por Man Utd » Dom Jul 14, 2013 23:45
- 5 Respostas
- 15042 Exibições
- Última mensagem por Man Utd

Seg Jul 15, 2013 23:55
Cálculo: Limites, Derivadas e Integrais
-
- Função Modular - dúvida
por jamiel » Qui Abr 28, 2011 13:11
- 18 Respostas
- 15450 Exibições
- Última mensagem por jamiel

Qui Mai 05, 2011 14:08
Funções
-
- Função modular - Dúvida
por Danilo » Dom Mar 10, 2013 15:50
- 1 Respostas
- 1519 Exibições
- Última mensagem por e8group

Dom Mar 10, 2013 16:49
Funções
-
- [Função modular] Dúvida com relação a raízes
por exburro » Sáb Mar 31, 2012 01:23
- 1 Respostas
- 2586 Exibições
- Última mensagem por LuizAquino

Sex Abr 06, 2012 12:40
Funções
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7384 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![f(x) = \sqrt[3]{x} f(x) = \sqrt[3]{x}](/latexrender/pictures/ac64ffeed293f17398e36ce96a633821.png) não é derivável em x= 0 , o limite das retas tangente a função neste ponto é o próprio
não é derivável em x= 0 , o limite das retas tangente a função neste ponto é o próprio  , o coeficiente angular desta reta vai
, o coeficiente angular desta reta vai  quado
quado  .
.
 , entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.
, entretanto a função não tem bico em x = 0. Analise o gráfico desta função representado abaixo.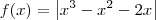 temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):
temos bicos em todas as raízes. Para verificar isso, confira os limites abaixo (o cálculo deles fica como exercício para você):