 por Cleyson007 » Sex Jun 14, 2013 15:19
por Cleyson007 » Sex Jun 14, 2013 15:19
Simplifique a expressão

Gabarito: K².K !
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por e8group » Sex Jun 14, 2013 16:13
por e8group » Sex Jun 14, 2013 16:13
Cleyson007 lembre-se que
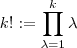
.Assim ,
![(k!)^3 = k^3[(k-1)!]^3 = [(k-1)!]^2 \cdot k^2 \cdot k(k-1)! (k!)^3 = k^3[(k-1)!]^3 = [(k-1)!]^2 \cdot k^2 \cdot k(k-1)!](/latexrender/pictures/ba9d3c1eefeb2b5b1f77c10fa9c96fde.png)
.Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Sex Jun 14, 2013 16:39
por Cleyson007 » Sex Jun 14, 2013 16:39
Santhiago, consegui entender essa igualdade (k!)³ = k³ [(k - 1)!]³. Não consegui entender a outra igualdade

Pode me explicar?
No aguardo,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por e8group » Sex Jun 14, 2013 17:05
por e8group » Sex Jun 14, 2013 17:05
Você comprende esta igualdade
![(k!)^3 = [k(k-1)!]^3 = k^3[(k-1)!]^3 (k!)^3 = [k(k-1)!]^3 = k^3[(k-1)!]^3](/latexrender/pictures/efb9b26ee660351fca2f3907c984d1e0.png)
? Se sim,podemos prosseguir ,note que
![[(k-1)!]^3 = (k-1)![(k-1)!]^2 [(k-1)!]^3 = (k-1)![(k-1)!]^2](/latexrender/pictures/fb84cdab4edc136eb5b6275dabefbd44.png)
Logo ,
![k^3[(k-1)!]^3 = k^3((k-1)![(k-1)!]^2) = k^2\cdot k ((k-1)![(k-1)!]^2) = k^2[(k-1)!]^2(k(k-1)!) k^3[(k-1)!]^3 = k^3((k-1)![(k-1)!]^2) = k^2\cdot k ((k-1)![(k-1)!]^2) = k^2[(k-1)!]^2(k(k-1)!)](/latexrender/pictures/3208ce9bb2426ffee40f1789902aa26e.png)
.
Mas ,
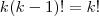
. Portanto ,
![(k!)^3 = k! \cdot k^2 [(k-1)!]^2 (k!)^3 = k! \cdot k^2 [(k-1)!]^2](/latexrender/pictures/cb3aae247313e4ea5e6bc959a30efe48.png)
.Qualquer dúvida estou à disposição .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Sex Jun 14, 2013 17:15
por Cleyson007 » Sex Jun 14, 2013 17:15
Consegui entender perfeitamente. Obrigado pela excelente explicação Santhiago!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2359 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2878 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- Fatorial
por elisonsevalho » Sex Mar 05, 2010 17:22
- 3 Respostas
- 2421 Exibições
- Última mensagem por Molina

Sáb Mar 06, 2010 14:49
Álgebra Elementar
-
- Fatorial.
por vanessasuellen » Qua Set 07, 2011 21:37
- 1 Respostas
- 1727 Exibições
- Última mensagem por Aliocha Karamazov

Sex Set 09, 2011 01:36
Estatística
-
- Fatorial de 0
por Neperiano » Qua Set 14, 2011 19:45
- 16 Respostas
- 9600 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 15:48
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




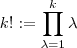 .Assim ,
.Assim , ![(k!)^3 = k^3[(k-1)!]^3 = [(k-1)!]^2 \cdot k^2 \cdot k(k-1)! (k!)^3 = k^3[(k-1)!]^3 = [(k-1)!]^2 \cdot k^2 \cdot k(k-1)!](/latexrender/pictures/ba9d3c1eefeb2b5b1f77c10fa9c96fde.png) .Tente concluir .
.Tente concluir .


![(k!)^3 = [k(k-1)!]^3 = k^3[(k-1)!]^3 (k!)^3 = [k(k-1)!]^3 = k^3[(k-1)!]^3](/latexrender/pictures/efb9b26ee660351fca2f3907c984d1e0.png) ? Se sim,podemos prosseguir ,note que
? Se sim,podemos prosseguir ,note que ![[(k-1)!]^3 = (k-1)![(k-1)!]^2 [(k-1)!]^3 = (k-1)![(k-1)!]^2](/latexrender/pictures/fb84cdab4edc136eb5b6275dabefbd44.png)
![k^3[(k-1)!]^3 = k^3((k-1)![(k-1)!]^2) = k^2\cdot k ((k-1)![(k-1)!]^2) = k^2[(k-1)!]^2(k(k-1)!) k^3[(k-1)!]^3 = k^3((k-1)![(k-1)!]^2) = k^2\cdot k ((k-1)![(k-1)!]^2) = k^2[(k-1)!]^2(k(k-1)!)](/latexrender/pictures/3208ce9bb2426ffee40f1789902aa26e.png) .
.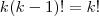 . Portanto ,
. Portanto , ![(k!)^3 = k! \cdot k^2 [(k-1)!]^2 (k!)^3 = k! \cdot k^2 [(k-1)!]^2](/latexrender/pictures/cb3aae247313e4ea5e6bc959a30efe48.png) .Qualquer dúvida estou à disposição .
.Qualquer dúvida estou à disposição .

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
