se A ou B é uma matriz não inversível então A.B também não é, Prove isto sem usar determinantes.
Como vou provar isso, sem usar um caso particular, por exemplo eu usei esse produto das duas matrizes respectivamente A e B.
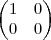

Que realizando o produto resulataria na matriz nulo, e seu determinante seria nulo, portanto não apresentaria tbm inversão.
Mas como vou provar isso sem usar determinantes??


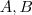 matrizes
matrizes 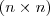 e
e  .
. solução do sistema
solução do sistema  .Multiplicando-se pela esquerda ambos lados da igualdade por
.Multiplicando-se pela esquerda ambos lados da igualdade por  ,aplicando a propriedade associativa e considerando
,aplicando a propriedade associativa e considerando  ,temos :
,temos : 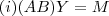 .Agora para mostrar que
.Agora para mostrar que 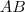 não é invertível basta mostrar que o sistema
não é invertível basta mostrar que o sistema 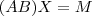 admite outra solução .Para isto ,considere
admite outra solução .Para isto ,considere  outra solução do sistema
outra solução do sistema  (note que podemos usar que o sistema
(note que podemos usar que o sistema  admite outra solução, pois ,por hipótese
admite outra solução, pois ,por hipótese  . Agora você pode concluir .
. Agora você pode concluir .


 , avisa que eu resolvo.
, avisa que eu resolvo.

