 por leha » Dom Nov 08, 2009 22:58
por leha » Dom Nov 08, 2009 22:58
Pessoal não estou conseguindo fazer essa integral. So uma observação. O a² na verdade é x² e o div e dividido.
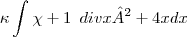
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Molina » Seg Nov 09, 2009 12:35
por Molina » Seg Nov 09, 2009 12:35
Bom dia Leha.
Confirme se é isso:
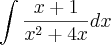

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por leha » Seg Nov 09, 2009 14:57
por leha » Seg Nov 09, 2009 14:57
è isso mesmo meu amigo molina. Desculpa é que eu não sei mexer no editor para sair assim como voce postou.
E agora como eu resolvo isso. Abraço
Tem essa aqui tambem eu não consigo.
K= 3x+1/(x+2)(x²+9)dx. So falta a integral na frente do K. Abraço
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por Molina » Seg Nov 09, 2009 15:09
por Molina » Seg Nov 09, 2009 15:09
Opa!
Ambas as questões que você postou acho que o melhor (diga-se mais fácil) jeito de resolver é por
integrais por frações parciais. Você já estudou este método?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por leha » Seg Nov 09, 2009 15:13
por leha » Seg Nov 09, 2009 15:13
Sim estou estudando mas tenho duvidas em relação de quando eu vou saber se é uma função racional propria ou não e o grau
dela. Poderia me dar um exemplo para eu começar a calcular. E tambem como eu vou calcular uma irracional. Posso aplicar o mesmo metodo???Obrigado.
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por leha » Seg Nov 09, 2009 16:00
por leha » Seg Nov 09, 2009 16:00
Meu amigo na questão j= integral de x+1/x²+4x escreveria assim??
j=A/x²+4x + B/x²+4x. Seria isso o inicio??
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por thadeu » Seg Nov 09, 2009 20:25
por thadeu » Seg Nov 09, 2009 20:25
Você tem que fazer a igualdade das frações:
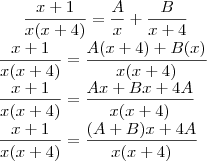
Os denominadores já são iguais, só falta igualar os numeradores:

Então, teremos a igualdade:

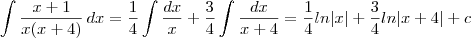
Veja se é essa a resposta
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por leha » Seg Nov 09, 2009 23:14
por leha » Seg Nov 09, 2009 23:14
Meu amigo comparando com o seu resultado surgiu uma duvida. No caso da integral no denominador e x²+4x. Porque voce ocultou o x². Abraço
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por thadeu » Ter Nov 10, 2009 11:49
por thadeu » Ter Nov 10, 2009 11:49
Não ocultei, coloquei x em evidência, então

-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por leha » Ter Nov 10, 2009 21:55
por leha » Ter Nov 10, 2009 21:55
Alguem pode me ajudar
Determine a decomposição em frações parciais do integrando e calcule a integral.
L=integral 2x+1/ (x+2)(x-1)(x-2)². Minha dificuldade e decompor o denominador depois disso eu consigo fazer.
Abraço
-
leha
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Jun 09, 2009 20:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: informatica
- Andamento: cursando
 por tamborex » Qui Nov 26, 2009 11:37
por tamborex » Qui Nov 26, 2009 11:37
DAE pessoal, estou com um problema numa integral aqui. Já tentei encontrar a resolução dela, mas se alguém souber como começar a resolver já ajuda. Usei a tranformação trigonométrica, mas emperrei, se usar frações parciais não dá pois as raízes são imaginárias.
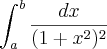
Detalhe, o que dificulta mesmo é o QUADRADO do lado de fora do parênteses.
Se alguém souber, pleeeease, manda a resposta!
-
tamborex
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 26, 2009 11:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
 por thadeu » Qui Nov 26, 2009 13:46
por thadeu » Qui Nov 26, 2009 13:46
-
thadeu
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Out 19, 2009 14:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por tamborex » Qui Nov 26, 2009 22:52
por tamborex » Qui Nov 26, 2009 22:52
MUITO OBRIGADO Thadeu!!! VAleu mesmo! Me ajudou pra caramba!
Realmente eu cheguei no começo da resolução, depois emperrei. O que faltou mesmo foi arroz com feijão de Trigonometria.
Com certeza vou ter que treinar mais pra conseguir resolver integrais mais complexas!!!
Valeu mesmo!!! Obrigado! : -)
-
tamborex
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 26, 2009 11:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ache a soma
por Balanar » Qua Ago 25, 2010 14:37
- 1 Respostas
- 1594 Exibições
- Última mensagem por Molina

Qua Ago 25, 2010 19:30
Desafios Difíceis
-
- Ache as raízes
por ALININA » Sáb Ago 13, 2011 07:53
- 1 Respostas
- 1442 Exibições
- Última mensagem por Neperiano

Dom Ago 14, 2011 13:20
Polinômios
-
- F(a) = G(a), ache o valor de a.
por teusfon » Qui Abr 19, 2012 11:23
- 1 Respostas
- 1288 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 13:02
Funções
-
- Ache o dominio
por angelmix » Sex Jul 27, 2012 14:49
- 3 Respostas
- 3028 Exibições
- Última mensagem por e8group

Ter Jul 31, 2012 10:58
Funções
-
- ache o valor de x
por Crist » Ter Nov 20, 2012 09:16
- 2 Respostas
- 1281 Exibições
- Última mensagem por Cleyson007

Ter Nov 20, 2012 09:47
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
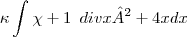


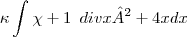

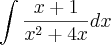







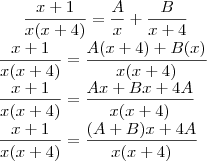


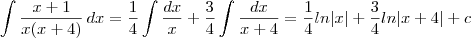





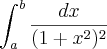

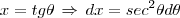 , temos:
, temos: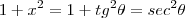
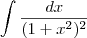
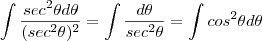

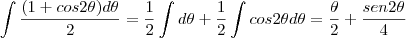
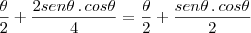
 , precisamos do triângulo retângulo abaixo:
, precisamos do triângulo retângulo abaixo:





