 por Direito » Sáb Jun 01, 2013 18:49
por Direito » Sáb Jun 01, 2013 18:49
-
Direito
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qua Mar 13, 2013 00:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Jun 02, 2013 15:07
por e8group » Dom Jun 02, 2013 15:07
Com a relação que você postou , podemos determinar

e

da seguinte forma .
Suponha

,então :
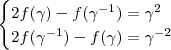
(Atenção !

) .
Multiplicando a 2ª equação por

e somando na primeira eq. obtemos ,
![2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}} 2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}}](/latexrender/pictures/bb7dc245b22c4d1d03c60afda9ada428.png)
.
Substituindo-se

na primeira ou segunda equação você encontra

. Depois basta fazer

ou

.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Jun 02, 2013 15:41
por e8group » Dom Jun 02, 2013 15:41
Ou melhor , multiplique a primeira equação por

e soma a segunda obtendo então :

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3424 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4192 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3137 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3387 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2994 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 e
e  da seguinte forma .
da seguinte forma .  ,então :
,então : 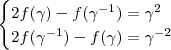 (Atenção !
(Atenção !  ) .
) .  e somando na primeira eq. obtemos ,
e somando na primeira eq. obtemos , ![2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}} 2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}}](/latexrender/pictures/bb7dc245b22c4d1d03c60afda9ada428.png) .
. na primeira ou segunda equação você encontra
na primeira ou segunda equação você encontra  . Depois basta fazer
. Depois basta fazer  ou
ou  .
. 
 e soma a segunda obtendo então :
e soma a segunda obtendo então :  .
.