



 e
e  da seguinte forma .
da seguinte forma .  ,então :
,então : 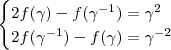 (Atenção !
(Atenção !  ) .
) .  e somando na primeira eq. obtemos ,
e somando na primeira eq. obtemos , ![2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}} 2f(\gamma) - f(\gamma^{-1}) + 2[2f(\gamma^{-1}) - f(\gamma)] = \gamma^{2} + 2\gamma^{-2} \implies 3 f(\gamma^{-1}) = \gamma^{2} + 2\gamma^{-2} \implies \boxed{f(\gamma^{-1}) = \frac{\gamma^{2} + 2\gamma^{-2} }{3}}](/latexrender/pictures/bb7dc245b22c4d1d03c60afda9ada428.png) .
. na primeira ou segunda equação você encontra
na primeira ou segunda equação você encontra  . Depois basta fazer
. Depois basta fazer  ou
ou  .
. 
 e soma a segunda obtendo então :
e soma a segunda obtendo então :  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)