Obs .: Foi mencionado que

divide

e

,mas isto não foi provado.Esta prova é simples,ela segue dos itens
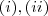
+ hipótese de

.De fato podemos usar
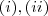
para provar que

divide
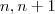
, assim , como

,pois :
![1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1) 1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1)](/latexrender/pictures/d118d4ca271f064e894e8bf387d555a0.png)
que resulta :


Agora,multiplicando

por

e

por

,obtemos
![(*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1 (*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1](/latexrender/pictures/8aae63593f20a9e8b46714a7ac599149.png)
![(**) 4[n(n+1)/2] -n(2n+1) = n (**) 4[n(n+1)/2] -n(2n+1) = n](/latexrender/pictures/be24982750669f68575f27a36aad710e.png)
Suponha que os números inteiros

sejam, respectivamente, o resultado da divisão de
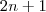
e

por

; assim multiplicando-se
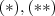
por

(é claro que
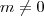
) obtemos ,

e

.
Como

então
![[(n+1)a - 4b] \in \mathbb{Z} [(n+1)a - 4b] \in \mathbb{Z}](/latexrender/pictures/87d596f8c1fa0ee620f5ce278d24822c.png)
o que implica

divide

.Analogamente ,chega-se a conclusão que

divide

.
Agora, basta utilizar este resultado + os itens
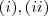
p/ concluir que
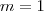
.Espero que ajude .
Por enquanto é isso que pensei em utilizar .


 é impar ; 2º) caso :
é impar ; 2º) caso : ![k[tex] tal que se [tex] n k[tex] tal que se [tex] n](/latexrender/pictures/2006e4268147d11421ceb66b0c35265e.png) é impar então
é impar então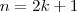 ;caso contrário
;caso contrário  . Tente analisar os dois casos .
. Tente analisar os dois casos .
 .Assim , se
.Assim , se  , então
, então  divide
divide 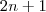 e
e  .Mas ,desde que
.Mas ,desde que  .Analisando ambos casos ,pela igualdade
.Analisando ambos casos ,pela igualdade 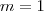 (pois caso contrário ele não dividiria ,
(pois caso contrário ele não dividiria , nem mesmo
nem mesmo  tal que
tal que  .
.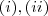 + hipótese de
+ hipótese de 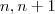 , assim , como
, assim , como  ,pois :
,pois :![1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1) 1 = 1 + 0 = 1 + [(2n) +(-2n)] = (1+2n)- 2(n) = 2(n+1) -(2n+1)](/latexrender/pictures/d118d4ca271f064e894e8bf387d555a0.png) que resulta :
que resulta : 

 por
por  por
por ![(*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1 (*) (n+1)(2n+1) - 4[(n)(n+1)/2] = n+1](/latexrender/pictures/8aae63593f20a9e8b46714a7ac599149.png)
![(**) 4[n(n+1)/2] -n(2n+1) = n (**) 4[n(n+1)/2] -n(2n+1) = n](/latexrender/pictures/be24982750669f68575f27a36aad710e.png)
 sejam, respectivamente, o resultado da divisão de
sejam, respectivamente, o resultado da divisão de 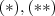 por
por  (é claro que
(é claro que 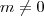 ) obtemos ,
) obtemos , 
 .
.  então
então ![[(n+1)a - 4b] \in \mathbb{Z} [(n+1)a - 4b] \in \mathbb{Z}](/latexrender/pictures/87d596f8c1fa0ee620f5ce278d24822c.png) o que implica
o que implica 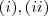 p/ concluir que
p/ concluir que 

 , avisa que eu resolvo.
, avisa que eu resolvo.

