Provar Propriedade Arquimediana: Para qualquer real x existe n E N/n>x
Podemos provar por absurdo por exemplo:
Se para algum x E R tivéssemos n<x, para todo n E N, então x é uma cota superior de N.
Como podemos provar isso passo a passo?
Grato!



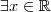 tal que
tal que  tem-se
tem-se  então
então  é limitado superiormente e possui uma cota superior .Consideremos
é limitado superiormente e possui uma cota superior .Consideremos a menor das cotas superiores .Como o número
a menor das cotas superiores .Como o número 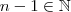 e
e 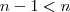 implica que este número não é limite superior de
implica que este número não é limite superior de  .Assim ,
.Assim , 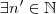 tal que
tal que  o que implica
o que implica  .Como
.Como 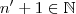 ,concluímos
,concluímos  não é majorante e também não pode ser a menor das cotas superiores de
não é majorante e também não pode ser a menor das cotas superiores de  e isto é uma contradição ,uma vez que consideremos
e isto é uma contradição ,uma vez que consideremos  como a menor das cotas superiores .Desta forma ,concluímos que
como a menor das cotas superiores .Desta forma ,concluímos que 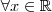 sempre existirá algum número natural
sempre existirá algum número natural 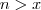 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes