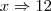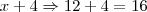"Os lados de um triangulo retangulo estão em progressão aritmética de razão 4. A soma de seus lados é igual a:
a)48 b)15 c)18 d)30 e)72"
Eu tentei fazer, achei os lados como sendo 4, 8 e 12 e na soma encontrei 24. O que será que eu estou fazendo de errado?
Muito obrigado, desde já, pela ajuda.
Marcelo.






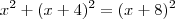
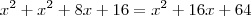

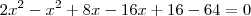




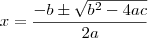
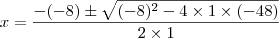


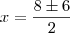
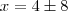


 , os lados serão:
, os lados serão:


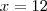 , de modo que os lados são:
, de modo que os lados são: