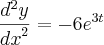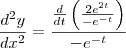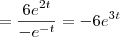por fabriel » Sex Mai 03, 2013 12:59
por fabriel » Sex Mai 03, 2013 12:59
Oi pessoal to com uma duvida no resultado aqui:
Exercicio: Seja C a curva com parametrização
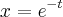
,
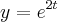
;
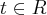
determine

e

Eu resolvi da seguinte maneira:

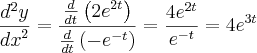
Até ai sem nenhum problema mas veja, se eu tivesse pegado a
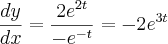
e logo em seguida derivasse isso olha o que aconteceria
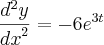
Que no caso é diferente do resultado que obtive na primeira resolução da derivada segunda, qual é que esta errada?
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Dom Mai 05, 2013 19:02
por young_jedi » Dom Mai 05, 2013 19:02
você teria que
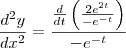
tente concluir e comente as duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fabriel » Seg Mai 06, 2013 01:41
por fabriel » Seg Mai 06, 2013 01:41
Não entendi muito bem essa passagem
young_jedi escreveu:você teria que
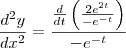
tente concluir e comente as duvidas
é muito confusa a derivada de funções dada na forma paramétrica, quando se trata na derivada de 2ª ordem pra frente
Mas se isso for o correto, então a resposta seria:

Que é bem diferente das respostas que obtive antes.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] FORMA PARAMÉTRICA
por fabriel » Qui Abr 25, 2013 17:43
- 2 Respostas
- 3047 Exibições
- Última mensagem por fabriel

Sex Abr 26, 2013 02:36
Cálculo: Limites, Derivadas e Integrais
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 3038 Exibições
- Última mensagem por lgbmp

Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
-
- derivada de ordem maior!
por giulioaltoe » Sex Jul 29, 2011 16:27
- 2 Respostas
- 1815 Exibições
- Última mensagem por giulioaltoe

Sex Jul 29, 2011 16:42
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:43
- 2 Respostas
- 2236 Exibições
- Última mensagem por spektroos

Dom Nov 25, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:48
- 1 Respostas
- 1554 Exibições
- Última mensagem por e8group

Dom Nov 25, 2012 10:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
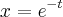 ,
, 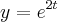 ;
; 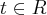 determine
determine  e
e 

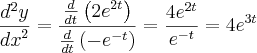
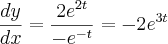 e logo em seguida derivasse isso olha o que aconteceria
e logo em seguida derivasse isso olha o que aconteceria