Há um problema, como já havia lhe dito, nessa questão. Não se pode garantir nada a parti da figura.
Dada a figura, temos as seguintes informações:
[*]Há uma parábola passando em

e em (talvez)

[*]Há uma reta que passa pelos pontos
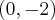
,

e por

Veja que a parábola passar em

quer dizer que

.
E se passa em

, então
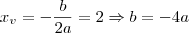
e

.
Logo, você tem

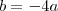

Tente em cima disso agora, e você encontrará todos os coeficientes. A equação resultante será

.
E para a reta, veja que
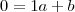
e

Portanto, os coeficientes da reta são

e

, ou seja, a equação da reta é

Para encontrar as coordenadas basta igualar as duas equações e fazer as manipulações necessárias.
A resposta é 24.
Desculpe a resposta resumida, mas acredito que devo lhe mostrar que existe ao menos um jeito de fazer. Te dei um caminho, agora tente segui-lo, entendê-lo e concluí-lo por sua conta...
Qualquer coisa estou a disposição...
Só os loucos sabem...

 e o
e o  .. sei também que
.. sei também que 
 e
e  .. e não consigo achar os valores. Agradecido
.. e não consigo achar os valores. Agradecido



 e em (talvez)
e em (talvez) 
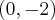 ,
, 
 .
.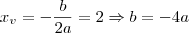
 .
.
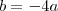

 .
.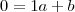

 e
e  , ou seja, a equação da reta é
, ou seja, a equação da reta é 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)