Assinale a solução geral do sistema linear representado pela matriz aumentada

a)

b)

c)
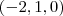
d)

A alternativa b e c são falsas; na matriz, nitidamente tenho apenas uma linha nula, o que vai nos dar uma variável independente e teremos como conjunto solução uma reta(que no ponto de vista geral, o sistema terá infinitas soluções). Cara, eu terminei de escalonar(pra matriz totalmente escalonada) a matriz e parametrizei as equações lineares:
~


Fazendo z = t (o parâmetro, ou seja, a variável livre.):

Dai o conjunto solução seria a reta:
 {
{ }
}Que não bate com nenhuma das alternativas do gabarito que é a alternativa a.
Mas vemos algo em comum na minha resposta com relação ao gabarito.
1)o vetor do espaço gerado é metade do que aparece no gabarito;
2) o vetor (-2,1,0) aparece no gabarito.
No que posso ter errado? Me corrijam, por favor. Qualquer ajuda é bem vinda. Grato desde já.


 é diretor da reta .Onde :
é diretor da reta .Onde : 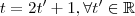 .
.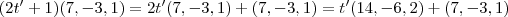 .
. 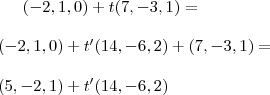 . Isto mostra que seus cálculos estão corretos .
. Isto mostra que seus cálculos estão corretos .
 e
e  qualquer vetor que é múltiplo escalar de
qualquer vetor que é múltiplo escalar de  será paralelo a
será paralelo a  obtemos que o ponto
obtemos que o ponto 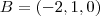 pertence a reta ,por outro lado ,tomando-se
pertence a reta ,por outro lado ,tomando-se 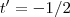 obterá
obterá  é múltiplo escalar de
é múltiplo escalar de 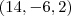 ,pelo argumento (*) ,podemos ver que a mudança de variável
,pelo argumento (*) ,podemos ver que a mudança de variável 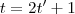 nos levará a resposta que está no formato do item (a) .
nos levará a resposta que está no formato do item (a) .