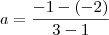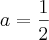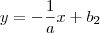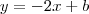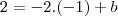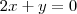por jordyson rocha » Seg Abr 29, 2013 17:16
por jordyson rocha » Seg Abr 29, 2013 17:16
Considerando-se o quadrado ABCD inscrito na circunferência de equação

e A(3,-1),pode-se afirmar que uma equação da reta que contém a diagonal BD é:
01) 3x - 2y - 7
02) 2y + x + 3
03) 2y - x + 5
04) 2x - y = 4
05) 2x + y = 0
Tentei de todos os jeitos mas acabo sempre na resposta errada a 03 . dá uma forcinha ai. muito obrigado.
-
jordyson rocha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Jan 30, 2013 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Seg Abr 29, 2013 20:49
por young_jedi » Seg Abr 29, 2013 20:49
primeiro vamos encontra a reta a equação da reta que contem a diagonal AC
sendo uma reta do tipo

temos que ela passa pelo centro da circunferencia portano ela contem os ponos A(3,-1) e O(1,-2)
então temos que
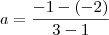
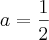
portanto a equção é do tipo

como a diagonal BD faz um angulo de 90º com a diagonal AC então ela é do tipo
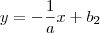
tente concluir a partir daqui e comente as duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por jordyson rocha » Qua Mai 15, 2013 09:22
por jordyson rocha » Qua Mai 15, 2013 09:22
olha eu não estou conseguindo achar o valor de "b" da fórmula tentei de todas maneiras mas não consegui.Preciso de ajuda.Obrigado
-
jordyson rocha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Jan 30, 2013 11:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Mai 15, 2013 21:46
por young_jedi » Qua Mai 15, 2013 21:46
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida uesb
por jordyson rocha » Sex Mar 01, 2013 18:32
- 3 Respostas
- 4169 Exibições
- Última mensagem por young_jedi

Sáb Mar 09, 2013 16:51
Matemática Financeira
-
- Dúvida uesb
por jordyson rocha » Sex Mar 01, 2013 19:10
- 1 Respostas
- 2687 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 23:58
Probabilidade
-
- Dúvida Uesb
por jordyson rocha » Sex Mar 01, 2013 21:02
- 1 Respostas
- 3031 Exibições
- Última mensagem por Russman

Sex Mar 01, 2013 21:47
Logaritmos
-
- Dúvida Uesb
por jordyson rocha » Seg Abr 22, 2013 19:08
- 0 Respostas
- 1456 Exibições
- Última mensagem por jordyson rocha

Seg Abr 22, 2013 19:08
Geometria Analítica
-
- DÚVIDA URGENTE!!
por tatahsooares » Seg Dez 13, 2010 01:32
- 0 Respostas
- 1397 Exibições
- Última mensagem por tatahsooares

Seg Dez 13, 2010 01:32
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e A(3,-1),pode-se afirmar que uma equação da reta que contém a diagonal BD é:
e A(3,-1),pode-se afirmar que uma equação da reta que contém a diagonal BD é: