Devemos encontrar valores em
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
que satisfaçam ao mesmo tempo as inequações que já foi mencionada .Vamos separar em dois casos .
Caso 1 : 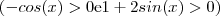 Caso 2 :
Caso 2 : 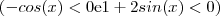
Em ambos casos a solução é a interseção entre os dois conjuntos ,se em um estágio obtemos que o conjunto

é solução da inequação
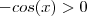
e

solução de

então a solução deste caso é a interseção entre os conjuntos .
Solução :
Caso 1: Como vc já adiantou ,
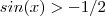
.P/ ficar mais claro ,faça um desenho do circulo trigonométrico em seu caderno e veja geometricamente que há dois valores em
![[0,\2pi] [0,\2pi]](/latexrender/pictures/6da9b3d7f48946780560913fed7d3009.png)
tal que
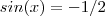
,um deles no 3° quadrante e o outro no 4° .Uma vez que encontramos estes valores é fácil obter o conjunto

solução de

.Para encontrar estes valores ,veja que :
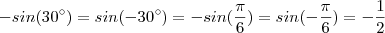
.
Usando que

e que
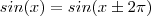
,obtemos que

(3° quadrante)
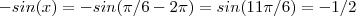
(4° quadrante)
Assim ,
![B =[0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] B =[0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi]](/latexrender/pictures/aeed585d86e85bc9a38f99b1cbc3cd29.png)
é o conjunto solução da desigualdade

.
Já em relação a outra desigualdade ,

.
Daí ,
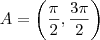
.
Portanto
![A \cap B = \left(\frac{\pi}{2} ,\frac{3\pi}{2}\right)\cap [0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] = \left(\frac{\pi}{2} , \frac{7\pi}{6} \right ) A \cap B = \left(\frac{\pi}{2} ,\frac{3\pi}{2}\right)\cap [0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] = \left(\frac{\pi}{2} , \frac{7\pi}{6} \right )](/latexrender/pictures/5a75dcec31118bdbe593b91d43e3fd7c.png)
. Assim ,qualquer valor que tomarmos neste intervalo ambas desigualdade serão satisfeitas (Verifique !!)
Agora tente concluir o caso 2 e comente as dúvidas .
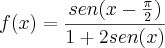 definida num subconjunto de
definida num subconjunto de ![\left[0,2\pi \right] \left[0,2\pi \right]](/latexrender/pictures/bba974a4663c6b343b265fc813462924.png) .É não negativa para todo
.É não negativa para todo  no intervalo:
no intervalo: .
.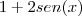 não consegui desenvolver.
não consegui desenvolver.

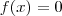 e
e 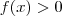 . No primeiro caso ,basta que o numerador se anule .Só p/ efeito de simplificação
. No primeiro caso ,basta que o numerador se anule .Só p/ efeito de simplificação  . Os pontos pertence ao intervalo [0,2\pi] em que
. Os pontos pertence ao intervalo [0,2\pi] em que 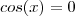 são
são  e
e  . No segundo caso ,
. No segundo caso ,  .
. 
 é um número positivo assim como
é um número positivo assim como 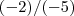 . Devemos encontrar valores em
. Devemos encontrar valores em ![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) que satisfazem
que satisfazem 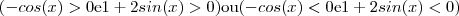 .Pense sobre isto . Comente as dúvidas .
.Pense sobre isto . Comente as dúvidas .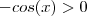 . o resultado seria que x e positivo no 1 e o 4 quadrante
. o resultado seria que x e positivo no 1 e o 4 quadrante o resultado deu
o resultado deu 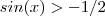 .
.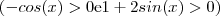
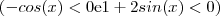
 é solução da inequação
é solução da inequação 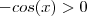 e
e  solução de
solução de  então a solução deste caso é a interseção entre os conjuntos .
então a solução deste caso é a interseção entre os conjuntos . 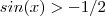 .P/ ficar mais claro ,faça um desenho do circulo trigonométrico em seu caderno e veja geometricamente que há dois valores em
.P/ ficar mais claro ,faça um desenho do circulo trigonométrico em seu caderno e veja geometricamente que há dois valores em ![[0,\2pi] [0,\2pi]](/latexrender/pictures/6da9b3d7f48946780560913fed7d3009.png) tal que
tal que 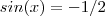 ,um deles no 3° quadrante e o outro no 4° .Uma vez que encontramos estes valores é fácil obter o conjunto
,um deles no 3° quadrante e o outro no 4° .Uma vez que encontramos estes valores é fácil obter o conjunto 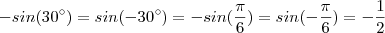 .
.  e que
e que 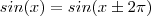 ,obtemos que
,obtemos que  (3° quadrante)
(3° quadrante)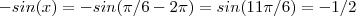 (4° quadrante)
(4° quadrante)![B =[0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] B =[0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi]](/latexrender/pictures/aeed585d86e85bc9a38f99b1cbc3cd29.png) é o conjunto solução da desigualdade
é o conjunto solução da desigualdade  .
. 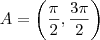 .
. ![A \cap B = \left(\frac{\pi}{2} ,\frac{3\pi}{2}\right)\cap [0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] = \left(\frac{\pi}{2} , \frac{7\pi}{6} \right ) A \cap B = \left(\frac{\pi}{2} ,\frac{3\pi}{2}\right)\cap [0,\frac{7\pi}{6}) \cup(\frac{11\pi}{6},2\pi] = \left(\frac{\pi}{2} , \frac{7\pi}{6} \right )](/latexrender/pictures/5a75dcec31118bdbe593b91d43e3fd7c.png) . Assim ,qualquer valor que tomarmos neste intervalo ambas desigualdade serão satisfeitas (Verifique !!)
. Assim ,qualquer valor que tomarmos neste intervalo ambas desigualdade serão satisfeitas (Verifique !!)
![-cos(x)<0\Rightarrow cos(x)>0\Rightarrow cos(x)>0 \Rightarrow\left[0 \right\frac{\pi}{2}[\cup \left]\frac {3\pi}{2}, \right 2\pi] -cos(x)<0\Rightarrow cos(x)>0\Rightarrow cos(x)>0 \Rightarrow\left[0 \right\frac{\pi}{2}[\cup \left]\frac {3\pi}{2}, \right 2\pi]](/latexrender/pictures/e4390bfbbc390d8acabced35ed7e243d.png) .
.![sin(x)>-\frac{-1}{2}\Rightarrow[0,\frac{7\pi}{6}[ \cup]\frac{11\pi}{6},2\pi] sin(x)>-\frac{-1}{2}\Rightarrow[0,\frac{7\pi}{6}[ \cup]\frac{11\pi}{6},2\pi]](/latexrender/pictures/d43bbc6f2b9cc727c6450987ab7fdd16.png)
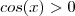 ,você acertou .Entretanto,a desigualdade
,você acertou .Entretanto,a desigualdade 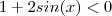 implica
implica 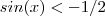 (e não implica
(e não implica 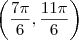 é o conjunto solução desta desigualdade .Porém , devemos tomar a interseção entre estes dois conjuntos para que ambas inequações sejam satisfeitas . Como
é o conjunto solução desta desigualdade .Porém , devemos tomar a interseção entre estes dois conjuntos para que ambas inequações sejam satisfeitas . Como ![\left(\frac{7\pi}{6} , \frac{11\pi}{6}\right) \cap \left[0, \frac{\pi}{2}\right)\cup \left(\frac{3\pi}{2}, 2\pi\right] = \left(\frac{3\pi}{2}, \frac{11\pi}{6}\right) \left(\frac{7\pi}{6} , \frac{11\pi}{6}\right) \cap \left[0, \frac{\pi}{2}\right)\cup \left(\frac{3\pi}{2}, 2\pi\right] = \left(\frac{3\pi}{2}, \frac{11\pi}{6}\right)](/latexrender/pictures/3ea531d6231b4b43f4fcdc69ab9066b8.png) ,concluímos que
,concluímos que  é o conjunto solução de
é o conjunto solução de 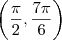 é o conjunto solução de
é o conjunto solução de 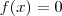 uma vez que
uma vez que  .
.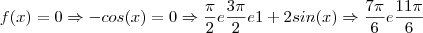
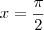 e
e 
