 por Viviani » Sáb Abr 27, 2013 14:40
por Viviani » Sáb Abr 27, 2013 14:40
-
Viviani
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jan 09, 2013 13:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Abr 27, 2013 15:00
por e8group » Sáb Abr 27, 2013 15:00
Observe que
![\frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3} \frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3}](/latexrender/pictures/30d908f380f4b2e50e9b037f923640a4.png)
. Assim ,
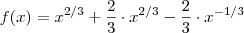
.
Podemos derivar a função aplicando a regra

em cada parcela .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Viviani » Sáb Abr 27, 2013 15:13
por Viviani » Sáb Abr 27, 2013 15:13
Mas no gabarito a resposta é
![f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}} f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}}](/latexrender/pictures/a301707f18aa53f986e4965166aa5439.png)
.
não estou conseguindo chegar nesse resultado :((
-
Viviani
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jan 09, 2013 13:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Abr 27, 2013 16:29
por e8group » Sáb Abr 27, 2013 16:29
É só uma questão de manipulação ,infelizmente a resposta não sai no formato do gabarito .Veja :
![f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]' f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]'](/latexrender/pictures/2e978aa673c8cd5d5206db82af549b40.png)
![f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]' f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]'](/latexrender/pictures/9de13757876ca12a7fd2fcdbb8e1a31a.png)
.
Vamos aplicar a regra de derivação
![[x^n]' = nx^{n-1} [x^n]' = nx^{n-1}](/latexrender/pictures/d38823bef1f4fb284cba3f431f64b7d7.png)
em cada expressão que está dentro de colchetes [] .Temos


.
Multiplicando "em cima " e "em baixo" por

segue o resultado do gabarito .
OBS_.: Poderia também aplicar a mesma regra de derivação a

e aplicar a regra do quociente em
![\frac{2(x-1)}{3\sqrt[3]{x}} \frac{2(x-1)}{3\sqrt[3]{x}}](/latexrender/pictures/547292a1fdf6cbffe37e37cfed8d4e72.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Viviani » Sáb Abr 27, 2013 17:29
por Viviani » Sáb Abr 27, 2013 17:29
ahh ta, ok, muito obrigada pela explicação !

-
Viviani
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Jan 09, 2013 13:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10881 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13187 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14793 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5111 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x):{x}^{\frac{2}{3}}+\frac{2(x-1)}{3\sqrt[3]{x}} f(x):{x}^{\frac{2}{3}}+\frac{2(x-1)}{3\sqrt[3]{x}}](/latexrender/pictures/5b03c1b3cb8840c1ffcf94b75f51d4bd.png)



![\frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3} \frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3}](/latexrender/pictures/30d908f380f4b2e50e9b037f923640a4.png) . Assim ,
. Assim , 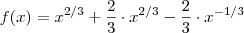 .
.  em cada parcela .
em cada parcela .
![f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}} f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}}](/latexrender/pictures/a301707f18aa53f986e4965166aa5439.png) .
.
![f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]' f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]'](/latexrender/pictures/2e978aa673c8cd5d5206db82af549b40.png)
![f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]' f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]'](/latexrender/pictures/9de13757876ca12a7fd2fcdbb8e1a31a.png) .
. ![[x^n]' = nx^{n-1} [x^n]' = nx^{n-1}](/latexrender/pictures/d38823bef1f4fb284cba3f431f64b7d7.png) em cada expressão que está dentro de colchetes [] .Temos
em cada expressão que está dentro de colchetes [] .Temos 
 .
.  segue o resultado do gabarito .
segue o resultado do gabarito . e aplicar a regra do quociente em
e aplicar a regra do quociente em ![\frac{2(x-1)}{3\sqrt[3]{x}} \frac{2(x-1)}{3\sqrt[3]{x}}](/latexrender/pictures/547292a1fdf6cbffe37e37cfed8d4e72.png) .
.

