![f(x):{x}^{\frac{2}{3}}+\frac{2(x-1)}{3\sqrt[3]{x}}](/latexrender/pictures/5b03c1b3cb8840c1ffcf94b75f51d4bd.png "f(x):{x}^{\frac{2}{3}}+\frac{2(x-1)}{3\sqrt[3]{x}}")
por e8group » Sáb Abr 27, 2013 15:00
![\frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3}](/latexrender/pictures/30d908f380f4b2e50e9b037f923640a4.png "\frac{2(x-1)}{3 \sqrt[3]{x}} = \frac{2x - 2}{3 x^(1/3)} = \frac{2}{3} \cdot \frac{x}{x^{1/3}} - \frac{2}{3} \cdot \frac{1}{x^{-1/3} }= \frac{2}{3} \cdot x^{1 - 1/3} - \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3} \cdot x^{2/3} - \frac{2}{3} \cdot x^{-1/3}")
. Assim ,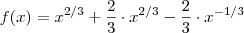 
. 
em cada parcela .
por Viviani » Sáb Abr 27, 2013 15:13
![f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}}](/latexrender/pictures/a301707f18aa53f986e4965166aa5439.png "f(x)=\frac{2(5x+1)}{9\sqrt[3]{{x}^{4}}}")
.por e8group » Sáb Abr 27, 2013 16:29
![f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]'](/latexrender/pictures/2e978aa673c8cd5d5206db82af549b40.png "f'(x) = [x^{2/3}+\frac{2}{3}x^{2/3} - \frac{2}{3}x^{-1/3}]' = [x^{2/3}] ' + [\frac{2}{3}x^{2/3}]' + [- \frac{2}{3}x^{-1/3}]'")
![f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]'](/latexrender/pictures/9de13757876ca12a7fd2fcdbb8e1a31a.png "f'(x) = [x^{2/3}] ' + \frac{2}{3}[x^{2/3}]' - \frac{2}{3} [x^{-1/3}]'")
. ![[x^n]' = nx^{n-1}](/latexrender/pictures/d38823bef1f4fb284cba3f431f64b7d7.png "[x^n]' = nx^{n-1}")
em cada expressão que está dentro de colchetes [] .Temos 
. 
segue o resultado do gabarito .
e aplicar a regra do quociente em ![\frac{2(x-1)}{3\sqrt[3]{x}}](/latexrender/pictures/547292a1fdf6cbffe37e37cfed8d4e72.png "\frac{2(x-1)}{3\sqrt[3]{x}}")
.Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)