 por Victor Gabriel » Sex Abr 26, 2013 20:51
por Victor Gabriel » Sex Abr 26, 2013 20:51
Olá pessoal boa noite, tem algum que pode mim ajuda nesta questão, olha com eu a fiz.
1º Calcule
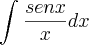
.
utilizei a tecnica da integração por parte:
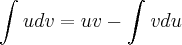
fazendo:

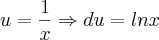
e

logo faço:
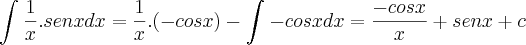
estou certo ou não?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Sex Abr 26, 2013 21:41
por e8group » Sex Abr 26, 2013 21:41
Acredito que não há funções elementares que derivando-se chega no integrando .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Gabriel » Sex Abr 26, 2013 22:22
por Victor Gabriel » Sex Abr 26, 2013 22:22
Santiago então como faço?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
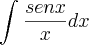 .
.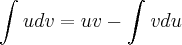

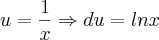 e
e  logo faço:
logo faço: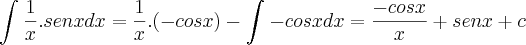

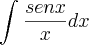 .
.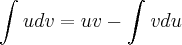

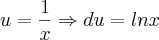 e
e  logo faço:
logo faço: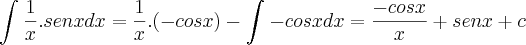



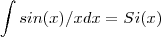 . Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .
. Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .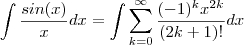 .Pela linearidade da integral ,
.Pela linearidade da integral , 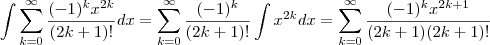


 .
.



