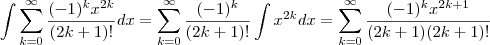por Victor Gabriel » Sex Abr 26, 2013 20:51
por Victor Gabriel » Sex Abr 26, 2013 20:51
Olá pessoal boa noite, tem algum que pode mim ajuda nesta questão, olha com eu a fiz.
1º Calcule
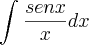
.
utilizei a tecnica da integração por parte:
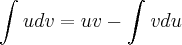
fazendo:

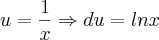
e

logo faço:
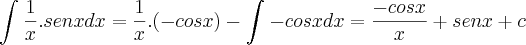
estou certo ou não?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Sex Abr 26, 2013 21:41
por e8group » Sex Abr 26, 2013 21:41
Acredito que não há funções elementares que derivando-se chega no integrando .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor Gabriel » Sex Abr 26, 2013 22:22
por Victor Gabriel » Sex Abr 26, 2013 22:22
Santiago então como faço?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
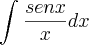 .
.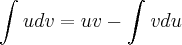

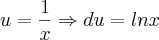 e
e  logo faço:
logo faço: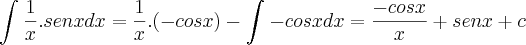

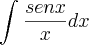 .
.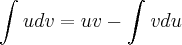

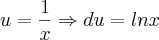 e
e  logo faço:
logo faço: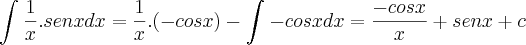



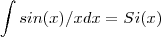 . Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .
. Veja : http://en.wikipedia.org/wiki/Trigonometric_integral .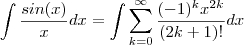 .Pela linearidade da integral ,
.Pela linearidade da integral ,