Então preciso calcular o comprimento da curva dada em forma parametrica:

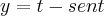 ,
, 
E calculando...
 e
e  .
.O comprimento da curva será dada pela integral:
![\int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt \int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt](/latexrender/pictures/0326152946a724f726af95322ae03ca3.png)
E arrumando essa integral teremos:
![\sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt \sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt](/latexrender/pictures/685793af19e5fad5ee7b073323be5965.png)
E ai que vem o problema, eu não consigo sair dessa integral, Ja tentei por partes e nada!!
Se puderem me ajudar eu agradeceria!!


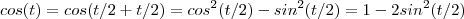 . Então :
. Então :  .
. 
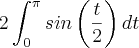
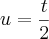 logo
logo 
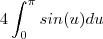



 +
+  (que está relacionada com o Teorema de Pitágoras ) consigo deduzir quase todas identidades .
(que está relacionada com o Teorema de Pitágoras ) consigo deduzir quase todas identidades . 
 .
.
 :
: