 por fabriel » Sex Abr 26, 2013 02:55
por fabriel » Sex Abr 26, 2013 02:55
E ai pessoal, blz. Estou com uma duvida na resolução!!
Então preciso calcular o comprimento da curva dada em forma parametrica:

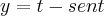
,

E calculando...

e

.
O comprimento da curva será dada pela integral:
![\int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt \int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt](/latexrender/pictures/0326152946a724f726af95322ae03ca3.png)
E arrumando essa integral teremos:
![\sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt \sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt](/latexrender/pictures/685793af19e5fad5ee7b073323be5965.png)
E ai que vem o problema, eu não consigo sair dessa integral, Ja tentei por partes e nada!!
Se puderem me ajudar eu agradeceria!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Sex Abr 26, 2013 11:47
por e8group » Sex Abr 26, 2013 11:47
Como
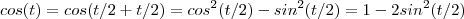
. Então :

.
Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Sex Abr 26, 2013 13:45
por fabriel » Sex Abr 26, 2013 13:45
Entendi, mas eu calculei e a resposta não bateu. Veja só:
Desejamos calcular essa integral
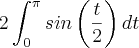
Chamando
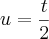
logo

Então
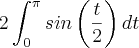
=
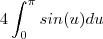
E resolvendo a integral obtemos:

E avaliando nos pontos 0 e pi, teremos a expressão:

Obrigado ai pela ajuda. O meu problema é que não estou muito familarizado com identidades trigonemétricas^^

Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Sex Abr 26, 2013 15:38
por e8group » Sex Abr 26, 2013 15:38
Só acrescentando
aqui fala sobre identidades trigonométricas .Pessoalmente não consigo lembrar de todas identidades ,mas apenas com as fórmulas

+
identidade trigonométrica fundamental
(que está relacionada com o Teorema de Pitágoras ) consigo deduzir quase todas identidades .
Fica a dica .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Sex Abr 26, 2013 19:06
por fabriel » Sex Abr 26, 2013 19:06
A resposta ta certa sim, erro meu.

Obrigado pela dica!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] dúvidas
por fabriel » Sáb Dez 14, 2013 21:12
- 4 Respostas
- 2240 Exibições
- Última mensagem por fabriel

Dom Dez 15, 2013 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Integral trigonometrica] - Dúvidas
por rafiusk » Qui Out 04, 2012 18:05
- 8 Respostas
- 3697 Exibições
- Última mensagem por rafiusk

Sáb Out 06, 2012 18:22
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Trigonométrica] Dúvidas.
por rafiusk » Dom Out 07, 2012 00:32
- 5 Respostas
- 2613 Exibições
- Última mensagem por rafiusk

Dom Out 07, 2012 17:31
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Duvidas na hora da substituição.
por fabriel » Sáb Out 06, 2012 03:26
- 5 Respostas
- 3255 Exibições
- Última mensagem por fabriel

Dom Nov 25, 2012 23:49
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL DEFINIDA] Duvidas na resolução
por fabriel » Sex Mar 22, 2013 13:09
- 1 Respostas
- 1428 Exibições
- Última mensagem por young_jedi

Sáb Mar 23, 2013 16:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

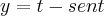 ,
, 
 e
e  .
.![\int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt \int_{0}^{\pi}\sqrt[]{{sen}^{2}t+{\left(1-{cos}^{2}t \right)}^{2}}dt](/latexrender/pictures/0326152946a724f726af95322ae03ca3.png)
![\sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt \sqrt[]{2}\int_{0}^{\pi}\sqrt[]{1-cos t}.dt](/latexrender/pictures/685793af19e5fad5ee7b073323be5965.png)


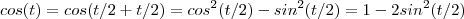 . Então :
. Então :  .
. 
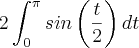
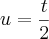 logo
logo 
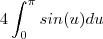



 +
+  (que está relacionada com o Teorema de Pitágoras ) consigo deduzir quase todas identidades .
(que está relacionada com o Teorema de Pitágoras ) consigo deduzir quase todas identidades . ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.