 por fabriel » Qui Abr 25, 2013 17:43
por fabriel » Qui Abr 25, 2013 17:43
E ai Pessoal blz?
Então estou em duvida nesse exercicio.
-- Calcular a derivada
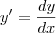
da seguinte função definida na forma paramétrica. Para quais valores de t, y' está definida?
Essa é a função dada na forma paramétrica:
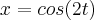
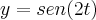
e isso para
![t\in\left[0,\frac{\pi}{2} \right] t\in\left[0,\frac{\pi}{2} \right]](/latexrender/pictures/89655ed5c73f7cdac67dc885da565d3c.png)
Calculei a derivada e deu:
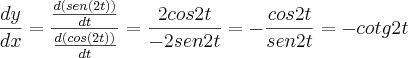
A minha duvida é nessa questão, como é que vou colocar

em função de x?
e mesmo se eu conseguir colocar, para quais valores de t, y' está definida, sendo que coloquei

em função de x?
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Qui Abr 25, 2013 21:24
por e8group » Qui Abr 25, 2013 21:24
Pensei de outra forma :
Pela regra da cadeia ,temos :
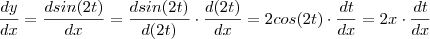
.
Mas ,
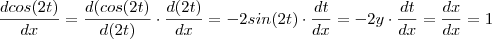
.
Para

podemos isolar
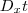
,

.
Daí ,
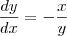
(Que é o que vc achou).
Mas pela identidade trigonométrica ,temos
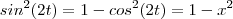
.E como ,
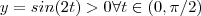
,
resulta
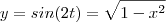
.
Assim ,

.
Se não errei algum cálculo acredito que seja isto .
Obs.: Da forma que vc fez está certo também ,só há um problema no intervalo
![[0,\pi/2] [0,\pi/2]](/latexrender/pictures/6b59bc315c28725e04e9331e71527914.png)
há dois valores que
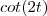
não está definido .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Sex Abr 26, 2013 02:36
por fabriel » Sex Abr 26, 2013 02:36
Entendo, obrigado!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA DE 2ª ORDEM] FORMA PARAMÉTRICA
por fabriel » Sex Mai 03, 2013 12:59
- 3 Respostas
- 1990 Exibições
- Última mensagem por young_jedi

Seg Mai 06, 2013 21:55
Cálculo: Limites, Derivadas e Integrais
-
- [Equaçao parametrica] Equacao parametrica com 3 pontos
por spektroos » Dom Mar 17, 2013 21:16
- 0 Respostas
- 1083 Exibições
- Última mensagem por spektroos

Dom Mar 17, 2013 21:16
Geometria Analítica
-
- Paramétrica da reta de um lado de um triangulo
por shantziu » Sáb Set 17, 2011 21:19
- 3 Respostas
- 5249 Exibições
- Última mensagem por Addlink1114

Qui Fev 18, 2016 06:22
Geometria Analítica
-
- AJUDA EQUAÇÃO VETORIAL/PARAMÉTRICA NO PLANO
 por Raquel Botura » Sex Nov 09, 2018 11:19
por Raquel Botura » Sex Nov 09, 2018 11:19
- 1 Respostas
- 8383 Exibições
- Última mensagem por Gebe

Sex Nov 09, 2018 17:13
Geometria Analítica
-
- Função de uma variavel (cartesiana, paramétrica e implícita)
por rhmgh » Dom Ago 12, 2012 21:20
- 3 Respostas
- 1806 Exibições
- Última mensagem por MarceloFantini

Qua Ago 15, 2012 10:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
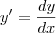 da seguinte função definida na forma paramétrica. Para quais valores de t, y' está definida?
da seguinte função definida na forma paramétrica. Para quais valores de t, y' está definida?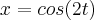
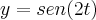
![t\in\left[0,\frac{\pi}{2} \right] t\in\left[0,\frac{\pi}{2} \right]](/latexrender/pictures/89655ed5c73f7cdac67dc885da565d3c.png)
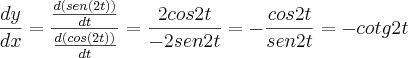
 em função de x?
em função de x? em função de x?
em função de x?

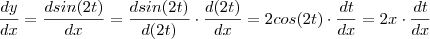 .
.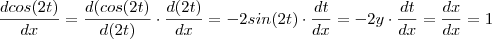 .
. podemos isolar
podemos isolar 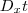 ,
, .
. 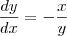 (Que é o que vc achou).
(Que é o que vc achou).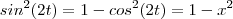 .E como ,
.E como , 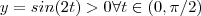 ,
, 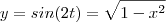 .
.  .
. ![[0,\pi/2] [0,\pi/2]](/latexrender/pictures/6b59bc315c28725e04e9331e71527914.png) há dois valores que
há dois valores que 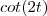 não está definido .
não está definido .


 , avisa que eu resolvo.
, avisa que eu resolvo.

