mede
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) . O volume do sólido gerado pela
. O volume do sólido gerado pela rotação deste triângulo em torno da hipotenusa é

cm¤. Determine os ângulos deste triângulo.
Fiz a rotação, percebi que forma 2 cones, mas dai travei

![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) . O volume do sólido gerado pela
. O volume do sólido gerado pela 

![\frac{r}{\sqrt[3]2}=\frac{x}{h} \frac{r}{\sqrt[3]2}=\frac{x}{h}](/latexrender/pictures/f6301daa4515fa9e949302ac78c02c7b.png)
![r=\frac{\sqrt[3]2x}{h} r=\frac{\sqrt[3]2x}{h}](/latexrender/pictures/7a24903437e8fd572b22006af915d47c.png)
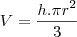
![\pi=\frac{h\pi}{3}.\frac{\sqrt[3]2^2.x^2}{h^2} \pi=\frac{h\pi}{3}.\frac{\sqrt[3]2^2.x^2}{h^2}](/latexrender/pictures/f7300efaaa9e5978e6a37a5255f26cbe.png)
![3h=\sqrt[3]2^2.x^2 3h=\sqrt[3]2^2.x^2](/latexrender/pictures/fb385d97ed8828fe1d0deed2a4a3d5bc.png)
![x^2=h^2-\sqrt[3]{2}^2 x^2=h^2-\sqrt[3]{2}^2](/latexrender/pictures/d0562d01e6e9fbe370a5fffcb78e32fa.png)
![3h=\sqrt[3]2^2.(h^2-\sqrt[3]{2}^2) 3h=\sqrt[3]2^2.(h^2-\sqrt[3]{2}^2)](/latexrender/pictures/efa2ca9cce2bc986caaa74742332102a.png)
![\sqrt[3]2^2h^2-3h-2\sqrt[3]{2}=0 \sqrt[3]2^2h^2-3h-2\sqrt[3]{2}=0](/latexrender/pictures/5348925eb9dd681155ee97ffccaec33f.png)
![h=\frac{4}{\sqrt[3]2^2} h=\frac{4}{\sqrt[3]2^2}](/latexrender/pictures/0ecb537acf45861485934d95976c6ed9.png)
![h=2\sqrt[3]2 h=2\sqrt[3]2](/latexrender/pictures/d584215ca5e8e89d4f597e8ca022dc5e.png)

 ... Tem alguma coisa a ver com a relação que você fez?
... Tem alguma coisa a ver com a relação que você fez?
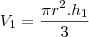
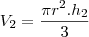
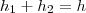
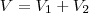
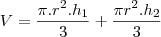
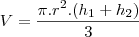
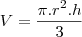



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)