 por Sohrab » Ter Abr 23, 2013 03:18
por Sohrab » Ter Abr 23, 2013 03:18
Estou em um exercício onde pede-se para calcular o seguinte limite:
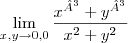
reescrevendo..

certo?
ai me disseram para usar o teorema do limite de função limitada vezes função que vai pra zero, que o limite daria zero..
mas cadê a função limitada ai? podem me ajudar? obrigado!!
edit: outra dúvida pertinente ao assunto.. como posso provar que um limite desse tipo não existe? Obrigado.
edit2: creio que a minha dificuldade esteja em 'perceber' e provar que uma função é limitada. como posso fazer isso?
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por young_jedi » Ter Abr 23, 2013 11:58
por young_jedi » Ter Abr 23, 2013 11:58
a função limitada é o seguinte

para qualquer que seja x ou y
então simplificando
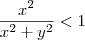
ou seja esta função é limitada ao valor 1 esse é o maximo valor que ela assume então no primeiro limite voce tem que
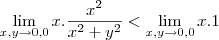
mais temos que

então
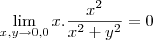
poceda de forma semelhante para o outro limite
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sohrab » Ter Abr 23, 2013 14:30
por Sohrab » Ter Abr 23, 2013 14:30
Entendo.. mas porque ela precisa ser limitada? Bastaria que o limite convergisse, não? porque ai seria 0*(algum número real) = 0
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por young_jedi » Ter Abr 23, 2013 20:18
por young_jedi » Ter Abr 23, 2013 20:18
sim, é exatamente isso que quer dizer limitada, significa que ela possui um valor maximo, ou seja multiplicada por zero resultara em zero
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sohrab » Qua Abr 24, 2013 01:12
por Sohrab » Qua Abr 24, 2013 01:12
young_jedi escreveu:a função limitada é o seguinte

para qualquer que seja x ou y
então simplificando
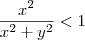
ou seja esta função é limitada ao valor 1 esse é o maximo valor que ela assume então no primeiro limite voce tem que
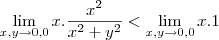
mais temos que

então
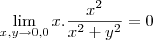
poceda de forma semelhante para o outro limite
estava aqui pensando.. como você sabe que a função é limitada superior e inferiormente por 1?
Porque veja..
para x e y diferentes de 0
y² > ou = 0
somando x²..
y² + x² > ou = 0 + x²
dividindo ambos os lados por x²+y²
1 > ou igual
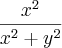
isso nos provou que ela é limitada superiormente (ou seja, é sempre menor do que 1)
ai tentei proceder assim para provar que ela é sempre maior do que -1 também:
|x|² = x²
então

e ai, fiz
=

< ou = 1
<=> -1 < ou igual
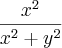
< ou igual 1
só que acho que está errada essa minha passagem, pois a desigualdade triangular diz que
|a+b| < ou igual |a|+|b|
ou eu posso fazer isso de passar o módulo para a fração toda, já que está tudo ao quadrado?
-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por young_jedi » Qua Abr 24, 2013 09:53
por young_jedi » Qua Abr 24, 2013 09:53
oque voce fez de passar o modulo sobre a fração toda é valido
mais repare que quaisquer que seja x e y a fração vai sempre resultar em um valor positivo portanto ela é sempre maior ou igual a 0 sendo assim seu limite inferior é 0 e não -1
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sohrab » Qui Abr 25, 2013 06:03
por Sohrab » Qui Abr 25, 2013 06:03
opa, tem razão.

-
Sohrab
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qui Mar 18, 2010 17:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Téc. em Mec. Usinagem e Info Programação
- Andamento: cursando
 por brunno10 » Qua Mai 01, 2013 00:28
por brunno10 » Qua Mai 01, 2013 00:28
Ola, pessoal!
gostaria de saber se voces tem alguma video-aula referente a como fazer o calculo do limite de uma função que apresente
quiciente indeterminado?
agradeço
-
brunno10
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mai 01, 2013 00:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITES função com duas variáveis, teo confronto
por inkz » Dom Nov 25, 2012 15:32
- 6 Respostas
- 9030 Exibições
- Última mensagem por e8group

Seg Nov 26, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Limites duas variaveis
por Razoli » Qui Jul 03, 2014 23:22
- 2 Respostas
- 2581 Exibições
- Última mensagem por Razoli

Qui Jul 03, 2014 23:41
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Equação de limite de duas variáveis reais
por Bianca_R » Dom Nov 04, 2012 21:45
- 1 Respostas
- 2155 Exibições
- Última mensagem por e8group

Seg Nov 05, 2012 11:19
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] - LIMITES DE DUAS VARIAVEIS
por Jol » Ter Fev 26, 2013 19:33
- 1 Respostas
- 1975 Exibições
- Última mensagem por young_jedi

Qua Fev 27, 2013 18:43
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6101 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
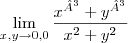




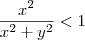
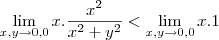

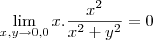

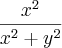

 < ou = 1
< ou = 1
