 se os números reais a , b , x e y satisfazem as equações :
se os números reais a , b , x e y satisfazem as equações : 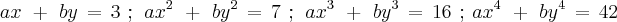
Resposta :
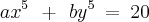
Obs: Não consegui enxergar nenhuma maneira de resolver.

 se os números reais a , b , x e y satisfazem as equações :
se os números reais a , b , x e y satisfazem as equações : 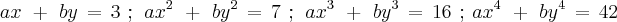
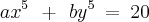

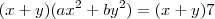
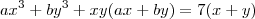
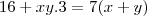
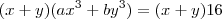
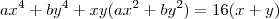

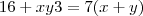

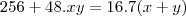
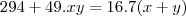


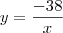
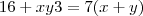 teremos
teremos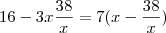
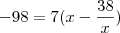
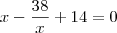
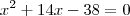
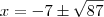
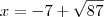 e substituindo na relação
e substituindo na relação 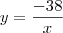
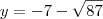
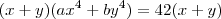
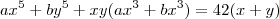
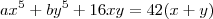
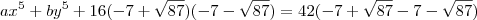
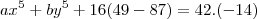
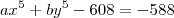
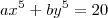


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante