 por laura1970 » Seg Abr 22, 2013 16:03
por laura1970 » Seg Abr 22, 2013 16:03
Boa tarde
estou tentando fazer estas expressões simplifica-las..mas não estou encontrando bom resultado:
a) (x+b)² - b² / (-x-2b)x
x²+2xb+b² /-x² -2bx
ai eu corto o x² com -x² depois 2xb - 2xb e tb +b² com - b²
deu 0...esta certo????
Letra b)
2x² + x - 1 / x- 1/2
2x² + x - 1/ 2x - 1/2
e dai não faço mais nada....
obrigada Lsm...
-
laura1970
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Fev 22, 2013 15:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: computação
- Andamento: cursando
 por Victor Gabriel » Seg Abr 22, 2013 21:00
por Victor Gabriel » Seg Abr 22, 2013 21:00
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por laura1970 » Seg Abr 22, 2013 21:26
por laura1970 » Seg Abr 22, 2013 21:26
Victor Gabriel
Muito obrigada pelo seu apoio. Me ajudou bastante...
Só que a letra b ...eu tenho que desenvolver o termina assim...Laura
-
laura1970
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Fev 22, 2013 15:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: computação
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- simplifique as expressões algébricas
por wattflix » Dom Out 04, 2015 17:12
- 1 Respostas
- 2043 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 21:43
Polinômios
-
- Simplifique as expressões e resolva a equação
por Dani da Silva » Qua Nov 27, 2013 18:55
- 1 Respostas
- 1591 Exibições
- Última mensagem por e8group

Qua Nov 27, 2013 20:08
Análise Combinatória
-
- Simplifique
por rodsales » Dom Ago 30, 2009 10:23
- 4 Respostas
- 12846 Exibições
- Última mensagem por Elcioschin

Dom Ago 30, 2009 14:32
Trigonometria
-
- fatorial simplifique:
por natanskt » Ter Dez 07, 2010 13:36
- 3 Respostas
- 8047 Exibições
- Última mensagem por Molina

Ter Jun 28, 2011 20:27
Binômio de Newton
-
- Simplifique a expressão:
por andersontricordiano » Dom Jan 22, 2012 22:03
- 2 Respostas
- 7383 Exibições
- Última mensagem por laura1970

Ter Jun 11, 2013 10:50
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



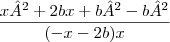


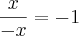
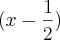 e (x+1), logo terei:
e (x+1), logo terei: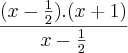 =x+1
=x+1