 por JessicaAraujo » Qui Abr 11, 2013 15:59
por JessicaAraujo » Qui Abr 11, 2013 15:59
Podem me ajudar?
Resolva a equação 2sec²(? - 3x) + 3 tan²(? - 3x) = 2, para x e R.
-
JessicaAraujo
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Abr 11, 2013 15:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qui Abr 11, 2013 18:09
por e8group » Qui Abr 11, 2013 18:09
Considere
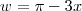
,temos então :
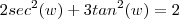
.
Ora ,mas pela identidade trigonométrica fundamental
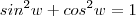
.Multiplicando ambos membros da equação por
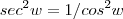
resulta
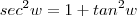
.Significa que podemos escrever
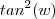
em função de
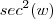
(e vice-versa) .
Desta forma ,ao substituirmos
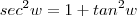
na equação
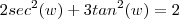
vamos ficar com
![2[1 +tan^2(w)] + 3tan^2(w) - 2 = 0 2[1 +tan^2(w)] + 3tan^2(w) - 2 = 0](/latexrender/pictures/092320083d9888c6aaaff1a86b7347af.png)
Ou ainda
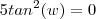
.
Tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por JessicaAraujo » Qui Abr 11, 2013 19:12
por JessicaAraujo » Qui Abr 11, 2013 19:12
Cheguei ao resultado:
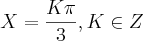
Correto?
-
JessicaAraujo
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Abr 11, 2013 15:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de uma equação.
por Danilo » Seg Out 19, 2015 15:51
- 1 Respostas
- 1649 Exibições
- Última mensagem por DanielFerreira

Sáb Out 31, 2015 20:08
Álgebra Elementar
-
- Resolução equação URGENTE
por jose84 » Ter Out 26, 2010 19:11
- 0 Respostas
- 1351 Exibições
- Última mensagem por jose84

Ter Out 26, 2010 19:11
Trigonometria
-
- [equaçao algebrica] travei na resoluçao
por vera lucia » Ter Set 20, 2011 00:08
- 2 Respostas
- 1620 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 18:38
Funções
-
- [equaçao algebrica] travei na resoluçao
por vera lucia » Ter Set 20, 2011 00:08
- 1 Respostas
- 1298 Exibições
- Última mensagem por Neperiano

Ter Set 20, 2011 13:13
Funções
-
- [Equação 1º Grau] - Dúvida na resolução
por FernandoBasso » Qua Set 21, 2011 08:54
- 1 Respostas
- 1622 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 16:13
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



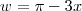 ,temos então :
,temos então : 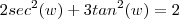 .
. 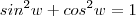 .Multiplicando ambos membros da equação por
.Multiplicando ambos membros da equação por 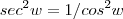 resulta
resulta 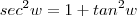 .Significa que podemos escrever
.Significa que podemos escrever 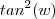 em função de
em função de 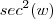 (e vice-versa) .
(e vice-versa) .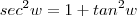 na equação
na equação 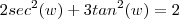 vamos ficar com
vamos ficar com ![2[1 +tan^2(w)] + 3tan^2(w) - 2 = 0 2[1 +tan^2(w)] + 3tan^2(w) - 2 = 0](/latexrender/pictures/092320083d9888c6aaaff1a86b7347af.png)
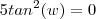 .
.
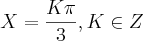


 .
.
 :
: