
O valor de x em função de a é:
A) a(3 -
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )
)B) a(2 -
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )
)C) a(1 +
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )
)D) a(2 +
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )
)E) a(3 +
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )
)Eu fiz da seguinte maneira:

onde calculei pitágoras
 =
= 
tentei várias vezes e não consegui. A resposta final tem que dar isso:
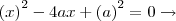 isolando o x temos x = a(2 -
isolando o x temos x = a(2 - ![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png) )..só que não consigo chegar à
)..só que não consigo chegar à 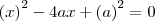


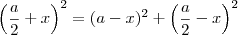
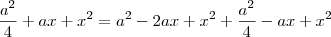

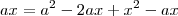


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)