 por rochadapesada » Seg Abr 08, 2013 21:48
por rochadapesada » Seg Abr 08, 2013 21:48
qual o volume de um tetraedro regular de 10 cm de altura?
Gabarito 125

Eu não consigo desenvolver ela... Fiz de tudo, coloquei altura como um dos catetos, acho a hipotenusa, mas com o valor não consigo encontrar a resposta
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Abr 10, 2013 15:21
por young_jedi » Qua Abr 10, 2013 15:21
um tetraedro regular tem quatro faces sendo que essas são triangulos equilateros, voce tem calcular a area de uma das faces para calcular o volume, como voce tem a altura do tetraedro voce é capaz de achar quanto vale os lados do tetraedro e assim calcular a area de sua base.
Se não conseguir encontrar o lado e a area comente.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Qua Abr 10, 2013 16:22
por rochadapesada » Qua Abr 10, 2013 16:22
Eu fiz já, coloquei a altura como cateto e coloquei

como outro cateto para achar a hipotenusa, mas fazendo isso acho um valor, mas com esse valor não dar o resultado... Depois eu coloquei a base com altura 10 cm (já que é um triângulo equilátero) e acho outro valor, mas não dar o resultado... como falei fiz de tudo =s
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Abr 10, 2013 16:34
por young_jedi » Qua Abr 10, 2013 16:34
eu pensei assim sendo o lado igual a l
temos que a medida do vertice da base ate o centro da base sera

então temos que
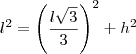
então

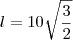
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Qua Abr 10, 2013 16:59
por rochadapesada » Qua Abr 10, 2013 16:59

Pq seria

, do vértice até o centro de um triângulo equilatero será sempre esse valor? Eu nunca vi e soube que do vértice até a base seria

, pois: do centro até a reta seria uma apótema, entao seria

, entao faria um pitágoras:

=
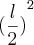
+

... mas com isso não daria

-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qua Abr 10, 2013 20:40
por young_jedi » Qua Abr 10, 2013 20:40
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por rochadapesada » Qua Abr 10, 2013 21:23
por rochadapesada » Qua Abr 10, 2013 21:23
agora entendi, obrigado pela paciência uahauhauhauha
-
rochadapesada
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Abr 04, 2013 22:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Espacial - Volume cilindro
por Reavourz » Qui Dez 11, 2014 10:24
- 1 Respostas
- 3743 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:13
Geometria Espacial
-
- [Geometria Espacial] Volume do tronco do cone
por jukkax » Sáb Out 19, 2013 21:32
- 1 Respostas
- 3565 Exibições
- Última mensagem por young_jedi

Dom Out 20, 2013 22:43
Geometria Espacial
-
- Volume do Tetraedro (SO)
por -civil- » Seg Ago 08, 2011 14:23
- 2 Respostas
- 3733 Exibições
- Última mensagem por -civil-

Ter Ago 09, 2011 12:30
Geometria Analítica
-
- [Planos e retas] Volume tetraedro
por ViniciusAlmeida » Sex Jul 17, 2015 10:50
- 0 Respostas
- 8091 Exibições
- Última mensagem por ViniciusAlmeida

Sex Jul 17, 2015 10:50
Geometria Analítica
-
- [Geometria Analítica] Vértices do tetraedro
por -civil- » Qua Ago 17, 2011 22:38
- 1 Respostas
- 2582 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 23:17
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 como outro cateto para achar a hipotenusa, mas fazendo isso acho um valor, mas com esse valor não dar o resultado... Depois eu coloquei a base com altura 10 cm (já que é um triângulo equilátero) e acho outro valor, mas não dar o resultado... como falei fiz de tudo =s
como outro cateto para achar a hipotenusa, mas fazendo isso acho um valor, mas com esse valor não dar o resultado... Depois eu coloquei a base com altura 10 cm (já que é um triângulo equilátero) e acho outro valor, mas não dar o resultado... como falei fiz de tudo =s

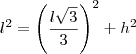

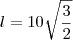

 Pq seria
Pq seria  , do vértice até o centro de um triângulo equilatero será sempre esse valor? Eu nunca vi e soube que do vértice até a base seria
, do vértice até o centro de um triângulo equilatero será sempre esse valor? Eu nunca vi e soube que do vértice até a base seria  , pois: do centro até a reta seria uma apótema, entao seria
, pois: do centro até a reta seria uma apótema, entao seria  , entao faria um pitágoras:
, entao faria um pitágoras: =
= 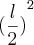 +
+  ... mas com isso não daria
... mas com isso não daria 


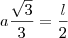







 .
.
 :
: