![\sqrt[2]{{x}^{2}-6x+k} \sqrt[2]{{x}^{2}-6x+k}](/latexrender/pictures/31716b1885aade6f30cd4148d988f551.png) , onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:
, onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:a) k
 5
5b)k=9
c)k=5
d)k
 9
9e)k
 9
9
![\sqrt[2]{{x}^{2}-6x+k} \sqrt[2]{{x}^{2}-6x+k}](/latexrender/pictures/31716b1885aade6f30cd4148d988f551.png) , onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:
, onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que: 5
5 9
9 9
9

 5, e a resposta é k
5, e a resposta é k 9 :s
9 :s
 estará bem definida
estará bem definida  existirem
existirem  e
e 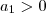 tal que a equação
tal que a equação 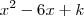 pode ser escrita como (i)
pode ser escrita como (i)  e (ii)
e (ii) .Desenvolvendo ambas expressões , e por igualdade de polinômios ,temos que :
.Desenvolvendo ambas expressões , e por igualdade de polinômios ,temos que : 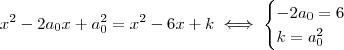 .Neste caso ,
.Neste caso ,  .
.  .Neste caso
.Neste caso  para qualquer
para qualquer 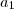 positivo ;logo , obrigatoriamente
positivo ;logo , obrigatoriamente  para a função
para a função estar bem definida .
estar bem definida . 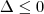 ou seja ,
ou seja , 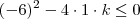 a função estaria bem definida nesta situação .
a função estaria bem definida nesta situação .

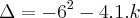
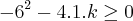



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)