 por Razoli » Sáb Abr 06, 2013 15:52
por Razoli » Sáb Abr 06, 2013 15:52
Pessoal como faço para zerar o "y" para que possa resolver a matriz e achar sua determinante por escalonamento?
| x 1 2 |
|0 x 2 |
|y 0 x |
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por e8group » Sáb Abr 06, 2013 18:28
por e8group » Sáb Abr 06, 2013 18:28
Por favor utilize o
para redigir sua matriz, Veja o código :
- Código: Selecionar todos
\begin{pmatrix} x & 1 & 2 \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix}
Resultado :
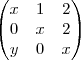
.
Assumindo que

poderemos aplicar algumas operações elementares ,
1)
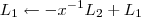

2)

![\begin{pmatrix} x & 1 & 2 \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ 0 & 0 & x -y\cdot x^{-1}[2 -2x^{-1}] \\ \end{pmatrix} \begin{pmatrix} x & 1 & 2 \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ 0 & 0 & x -y\cdot x^{-1}[2 -2x^{-1}] \\ \end{pmatrix}](/latexrender/pictures/ac09b4fc561877c36019b23d939d719a.png)
.
Editado pela última vez por
e8group em Sáb Abr 06, 2013 19:40, em um total de 1 vez.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Razoli » Sáb Abr 06, 2013 18:46
por Razoli » Sáb Abr 06, 2013 18:46
Muito Obrigado!! Me ajudou muito!!!
-
Razoli
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Abr 06, 2013 15:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por e8group » Sáb Abr 06, 2013 19:40
por e8group » Sáb Abr 06, 2013 19:40
Não há de que .Agora observei um erro de digitação , na última matriz o elemento 3,1 é na verdade 0 e não 1 . Já está Editado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7149 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- Matriz & Determinante
por Colton » Qua Out 13, 2010 12:56
- 1 Respostas
- 5094 Exibições
- Última mensagem por Colton

Qua Out 20, 2010 10:02
Matrizes e Determinantes
-
- matriz e determinante
por arianos » Qui Mai 10, 2012 14:56
- 6 Respostas
- 7192 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:15
Matrizes e Determinantes
-
- [Determinante de matriz]
por spektroos » Qui Nov 08, 2012 19:02
- 4 Respostas
- 5959 Exibições
- Última mensagem por spektroos

Qui Nov 08, 2012 19:35
Matrizes e Determinantes
-
- Determinante da matriz!
por Razoli » Seg Abr 08, 2013 00:10
- 1 Respostas
- 3176 Exibições
- Última mensagem por Razoli

Seg Abr 08, 2013 00:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 para redigir sua matriz, Veja o código :
para redigir sua matriz, Veja o código : 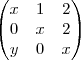 .
.  poderemos aplicar algumas operações elementares ,
poderemos aplicar algumas operações elementares , 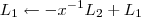


![\begin{pmatrix} x & 1 & 2 \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ 0 & 0 & x -y\cdot x^{-1}[2 -2x^{-1}] \\ \end{pmatrix} \begin{pmatrix} x & 1 & 2 \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ y & 0 & x \\ \end{pmatrix} \sim \begin{pmatrix} x & 0 & 2 -2x^{-1} \\ 0 & x & 2 \\ 0 & 0 & x -y\cdot x^{-1}[2 -2x^{-1}] \\ \end{pmatrix}](/latexrender/pictures/ac09b4fc561877c36019b23d939d719a.png) .
.

