O seu pensamento está correto.
Primeiro, você constrói o vetor
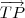
usando
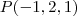
e
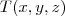
.
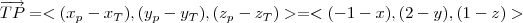
.
Agora, como você disse, esse vetor deve ser perpendicular a qualquer vetor pertencente ao plano. Isto é, o vetor
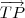
tem de ser paralelo ao vetor normal ao plano que é obtido pelos coeficientes da equação do plano.

.
Ou seja, o produto vetorial
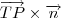
tem de ser nulo e , consequentemente, o vetor
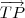
é um múltiplo do próprio vetor normal. Mas não qualquer múltiplo. Note que o módulo de
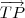
é exatamente a distância(definida perpendicularmente ao plano) entre o plano e o ponto P. Sabemos que esta é dada por
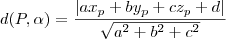
que pode ser calculada uma vez que conhecemos o ponto P. Vou chamar essa distância de

.
Portanto,

e, assim,
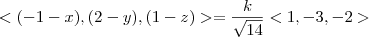
de onde
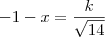
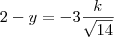
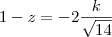
Agora basta você isolar as coordenadas de T.
(:
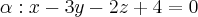 e o ponto P(-1;2;1). O exercício pede que determinemos as coordenadas do ponto T, pertencente ao plano
e o ponto P(-1;2;1). O exercício pede que determinemos as coordenadas do ponto T, pertencente ao plano  , e que está mais próximo do ponto P.
, e que está mais próximo do ponto P.

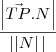
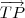 usando
usando 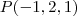 e
e 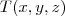 .
.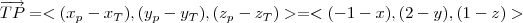 .
. .
. 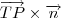 tem de ser nulo e , consequentemente, o vetor
tem de ser nulo e , consequentemente, o vetor 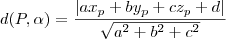
 .
.
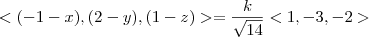
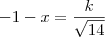
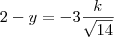
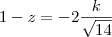



 , avisa que eu resolvo.
, avisa que eu resolvo.

