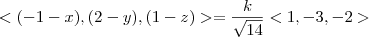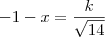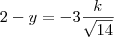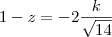por emsbp » Sáb Abr 06, 2013 16:34
por emsbp » Sáb Abr 06, 2013 16:34
Boa tarde. É dado a equação do plano
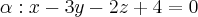
e o ponto P(-1;2;1). O exercício pede que determinemos as coordenadas do ponto T, pertencente ao plano

, e que está mais próximo do ponto P.
Sei que a distância mais próxima do ponto P terá de ser na perpendicular em relação a T. Comecei por pensar em formar o vetor TP, sendo T(x,y,z), mas a partir daí não estou a conseguir resolver.
Peço ajuda.
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por temujin » Sáb Abr 06, 2013 17:55
por temujin » Sáb Abr 06, 2013 17:55
Boa tarde.
Este vetor TP que vc tomou pode sempre ser decomposto em uma soma de 2 vetores: um paralelo ao vetor normal ao plano (que é a projeção ortogonal de TP sobre N) e outro paralelo ao próprio plano. A distância de P ao plano será, então, igual à norma da projeção ortogonal e é dada por:
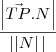
Acho que com isto vc consegue prosseguir, certo?
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Russman » Sáb Abr 06, 2013 18:42
por Russman » Sáb Abr 06, 2013 18:42
O seu pensamento está correto.
Primeiro, você constrói o vetor
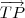
usando
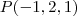
e
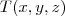
.
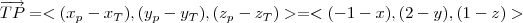
.
Agora, como você disse, esse vetor deve ser perpendicular a qualquer vetor pertencente ao plano. Isto é, o vetor
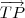
tem de ser paralelo ao vetor normal ao plano que é obtido pelos coeficientes da equação do plano.

.
Ou seja, o produto vetorial
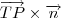
tem de ser nulo e , consequentemente, o vetor
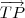
é um múltiplo do próprio vetor normal. Mas não qualquer múltiplo. Note que o módulo de
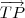
é exatamente a distância(definida perpendicularmente ao plano) entre o plano e o ponto P. Sabemos que esta é dada por
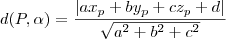
que pode ser calculada uma vez que conhecemos o ponto P. Vou chamar essa distância de

.
Portanto,

e, assim,
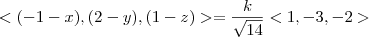
de onde
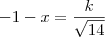
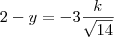
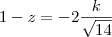
Agora basta você isolar as coordenadas de T.
(:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por emsbp » Dom Abr 07, 2013 16:37
por emsbp » Dom Abr 07, 2013 16:37
Boa tarde.
Muito obrigado. Já percebi.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto das coordenadas do ponto P.
por Lenin » Sex Mai 03, 2013 00:35
- 1 Respostas
- 1503 Exibições
- Última mensagem por young_jedi

Sáb Mai 04, 2013 00:42
Funções
-
- [Coordenadas de um ponto simetrico]
por lucasdemirand » Dom Set 01, 2013 11:40
- 1 Respostas
- 2385 Exibições
- Última mensagem por e8group

Ter Set 03, 2013 12:12
Álgebra Linear
-
- [Geometria Analítica] Vetores No Espaço
por felipe10 » Seg Mai 07, 2012 13:16
- 1 Respostas
- 5291 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 18:55
Geometria Analítica
-
- Geometria Analitica// Coordenadas polares
por duduxo81 » Sex Nov 18, 2016 13:20
- 0 Respostas
- 2497 Exibições
- Última mensagem por duduxo81

Sex Nov 18, 2016 13:20
Geometria Analítica
-
- geometria no plano e espaço - exercicios ajuda
 por mmartins » Seg Mai 03, 2010 08:22
por mmartins » Seg Mai 03, 2010 08:22
- 0 Respostas
- 1812 Exibições
- Última mensagem por mmartins

Seg Mai 03, 2010 08:22
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
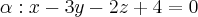 e o ponto P(-1;2;1). O exercício pede que determinemos as coordenadas do ponto T, pertencente ao plano
e o ponto P(-1;2;1). O exercício pede que determinemos as coordenadas do ponto T, pertencente ao plano  , e que está mais próximo do ponto P.
, e que está mais próximo do ponto P.

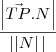
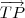 usando
usando 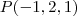 e
e 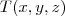 .
.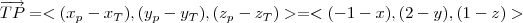 .
. .
. 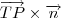 tem de ser nulo e , consequentemente, o vetor
tem de ser nulo e , consequentemente, o vetor 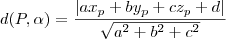
 .
.