por maumi » Sex Abr 05, 2013 19:25
1- tgh²x = sech²x
Tenho dúvidas quando é para verificar identidades de tangente hiperbólica e secante hiperbolica, não consigo igualar essa identidade. Desde já, obrigado.
-
maumi
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sex Abr 05, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Séries de Fourier de Funções Hiperbólicas
por clecio » Qua Abr 13, 2011 14:18
- 1 Respostas
- 2094 Exibições
- Última mensagem por LuizAquino
Qui Abr 14, 2011 23:32
Cálculo: Limites, Derivadas e Integrais
-
- Identidade Trigonometrica
por MERLAYNE » Ter Abr 24, 2012 19:40
- 4 Respostas
- 2278 Exibições
- Última mensagem por DanielFerreira
Ter Abr 24, 2012 20:12
Trigonometria
-
- Função Identidade
por Jhenrique » Sáb Nov 17, 2012 19:29
- 0 Respostas
- 1206 Exibições
- Última mensagem por Jhenrique
Sáb Nov 17, 2012 19:29
Funções
-
- [Integral] Identidade
por klueger » Seg Mar 04, 2013 17:52
- 1 Respostas
- 1514 Exibições
- Última mensagem por young_jedi
Seg Mar 04, 2013 23:28
Cálculo: Limites, Derivadas e Integrais
-
- verificar questão de probabilidade
por gutorocher » Qua Jul 21, 2010 21:59
- 7 Respostas
- 3782 Exibições
- Última mensagem por gutorocher
Sex Ago 13, 2010 15:51
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
Resposta:
Dica:
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a
e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![1 - tanh^2(x) = 1 - sech^2(x) sinh^2(x) = sech^2(x)[cosh^2(x) - sinh^2(x)]](/latexrender/pictures/46e0e3ccf673907be6566b36f67861e7.png "1 - tanh^2(x) = 1 - sech^2(x) sinh^2(x) = sech^2(x)[cosh^2(x) - sinh^2(x)]")
. 
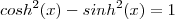e conclua que é verdadeiro a igualdade 
.