 por terraqueando » Qui Mar 28, 2013 00:27
por terraqueando » Qui Mar 28, 2013 00:27
Ei galera, to precisando muito da ajuda de vocês. Eu tenho esse trabalho pra entregar daqui exatamente uma semana no qual tá valendo 1/5 da nota. Não consigo nem começar o mesmo, gostaria muito da ajuda de vocês pra pelo menos começá-lo e algumas dicas para a resolução. Seria somente substituir o t por valores numéricos?
Esboce o gráfico da função
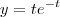
, com

. Esta função é uma função do tipo impulso

, onde
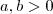
são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
-
terraqueando
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 28, 2013 00:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmácia
- Andamento: cursando
 por timoteo » Qui Mar 28, 2013 17:34
por timoteo » Qui Mar 28, 2013 17:34
Olá.
Essa função é uma exponencial, então, dê uma olhada em gráfico dessa função em livros ou na net.
Você pode também, fazer como função logarítmica, caso você sinta-se melhor com a álgebra desta.
É isso ai!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por terraqueando » Qua Abr 03, 2013 21:30
por terraqueando » Qua Abr 03, 2013 21:30
timoteo escreveu:Olá.
Essa função é uma exponencial, então, dê uma olhada em gráfico dessa função em livros ou na net.
Você pode também, fazer como função logarítmica, caso você sinta-se melhor com a álgebra desta.
É isso ai!
Meu professor disse que precisa fazer o esboço com derivada primeira, pra achar os pontos críticos e derivada segunda pra achar os pontos de inflexão, só que não to conseguindo :(
-
terraqueando
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 28, 2013 00:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmácia
- Andamento: cursando
 por Russman » Qua Abr 03, 2013 21:48
por Russman » Qua Abr 03, 2013 21:48
É recorrente a análise das derivadas de uma função para esboçar o gráfico da mesma. Em 1° lugar vamos analisar os pontos em que a função se anula e intersepta o eixo vertical.


Portanto o ponto
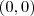
pertence a função é exatamente onde ela se anula e intersepta o eixo vertical. Agora vamos analisar se ela possui um ponto extremo. Este é tal que a 1° derivada da função se anula. Assim

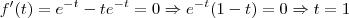
.
Portanto, temos um ponto de máximo em

pois no limite em que

calculamos que a função vai para

. Se calculamos o limite quando

vai para
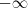
temos que a função tente também a
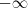
.
Assim, a função vem de
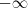
, passa pela origem, cresce até

e começa a decrescer atingindo assintoticamente o

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Concentração (Proporção)
por plugpc » Sáb Out 24, 2009 15:46
- 2 Respostas
- 2317 Exibições
- Última mensagem por plugpc

Seg Out 26, 2009 20:02
Álgebra Elementar
-
- Ajuda com exercicio!!!
por tuany » Seg Mar 24, 2008 15:34
- 3 Respostas
- 4117 Exibições
- Última mensagem por tuany

Ter Mar 25, 2008 16:50
Funções
-
- Ajuda com exercicio!!!
por karol_agnelli » Qua Mar 26, 2008 19:40
- 6 Respostas
- 7270 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 15:23
Tópicos sem Interação (leia as regras)
-
- ajuda com o exercicio
por Mimizinha » Seg Mar 31, 2008 18:19
- 2 Respostas
- 3493 Exibições
- Última mensagem por Mimizinha

Ter Abr 01, 2008 10:24
Geometria Plana
-
- Ajuda em Exercício.
 por Levi23 » Dom Set 28, 2008 02:01
por Levi23 » Dom Set 28, 2008 02:01
- 12 Respostas
- 8831 Exibições
- Última mensagem por admin

Sáb Out 04, 2008 13:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
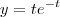 , com
, com  . Esta função é uma função do tipo impulso
. Esta função é uma função do tipo impulso  , onde
, onde 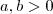 são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
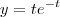 , com
, com  . Esta função é uma função do tipo impulso
. Esta função é uma função do tipo impulso  , onde
, onde 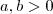 são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).




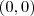 pertence a função é exatamente onde ela se anula e intersepta o eixo vertical. Agora vamos analisar se ela possui um ponto extremo. Este é tal que a 1° derivada da função se anula. Assim
pertence a função é exatamente onde ela se anula e intersepta o eixo vertical. Agora vamos analisar se ela possui um ponto extremo. Este é tal que a 1° derivada da função se anula. Assim
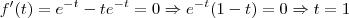 .
. pois no limite em que
pois no limite em que  calculamos que a função vai para
calculamos que a função vai para  . Se calculamos o limite quando
. Se calculamos o limite quando  vai para
vai para 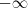 temos que a função tente também a
temos que a função tente também a 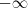 .
. 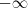 , passa pela origem, cresce até
, passa pela origem, cresce até  e começa a decrescer atingindo assintoticamente o
e começa a decrescer atingindo assintoticamente o  .
.