Esboce o gráfico da função
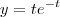 , com
, com  . Esta função é uma função do tipo impulso
. Esta função é uma função do tipo impulso  , onde
, onde 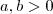 são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
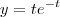 , com
, com  . Esta função é uma função do tipo impulso
. Esta função é uma função do tipo impulso  , onde
, onde 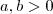 são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).
são constantes. Este tipo de função serve, por exemplo, para aproximar o que ocorre com a concentração y da droga paracetamol no sangue no tempo t(t horas).

timoteo escreveu:Olá.
Essa função é uma exponencial, então, dê uma olhada em gráfico dessa função em livros ou na net.
Você pode também, fazer como função logarítmica, caso você sinta-se melhor com a álgebra desta.
É isso ai!



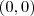 pertence a função é exatamente onde ela se anula e intersepta o eixo vertical. Agora vamos analisar se ela possui um ponto extremo. Este é tal que a 1° derivada da função se anula. Assim
pertence a função é exatamente onde ela se anula e intersepta o eixo vertical. Agora vamos analisar se ela possui um ponto extremo. Este é tal que a 1° derivada da função se anula. Assim
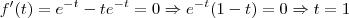 .
. pois no limite em que
pois no limite em que  calculamos que a função vai para
calculamos que a função vai para  . Se calculamos o limite quando
. Se calculamos o limite quando  vai para
vai para  temos que a função tente também a
temos que a função tente também a  .
. 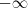 , passa pela origem, cresce até
, passa pela origem, cresce até  e começa a decrescer atingindo assintoticamente o
e começa a decrescer atingindo assintoticamente o  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

