 por xafabi » Ter Abr 02, 2013 23:03
por xafabi » Ter Abr 02, 2013 23:03
Ola pessoal, tentei rwsolver essas questões mas não consegui, se alguem puder ajudar agradeço muito
1) Calcule : dy/dx:
a) y = e^x/sqrt x
b) y = e^x (senx + \cos x)
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Qua Abr 03, 2013 12:09
por young_jedi » Qua Abr 03, 2013 12:09
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por xafabi » Qua Abr 03, 2013 15:35
por xafabi » Qua Abr 03, 2013 15:35
Ola amigo muito obrigado pela primeira, por favor veja se a segunda esta correta ou fiz alguma coisa errada
dy/ dx = [e^x (sen x + cosx) - (cosx - senx)e^x] / (senx + cosx)^2 = (2e^x * senx) / ( senx + cosx)^2
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Qua Abr 03, 2013 16:37
por young_jedi » Qua Abr 03, 2013 16:37
a equação é esta ?
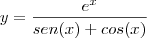
se for esta correto
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por xafabi » Qua Abr 03, 2013 17:02
por xafabi » Qua Abr 03, 2013 17:02
Ola amigo não é divisão
b) y = e^x (senx + cos x)
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Qua Abr 03, 2013 17:51
por young_jedi » Qua Abr 03, 2013 17:51
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por xafabi » Qua Abr 03, 2013 21:12
por xafabi » Qua Abr 03, 2013 21:12
Amigo voçe ajudou demais muito obrigado
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2264 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7482 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4960 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2972 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1997 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



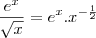
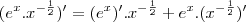
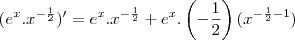
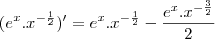


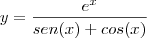


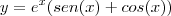
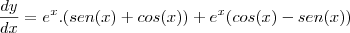
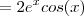


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.