 por Douglas16 » Sáb Mar 30, 2013 13:16
por Douglas16 » Sáb Mar 30, 2013 13:16
Determinar as condições para as constantes

,

,

e


tal que
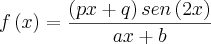
satisfaça
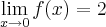
e
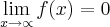
.
Minha solução inacabada:
Desde que :
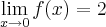
portanto

e;

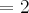
, portanto

, portanto
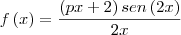
e;
de

, só sei que devo eliminar esta indeterminação, só não sei como.
Editado pela última vez por
Douglas16 em Dom Mar 31, 2013 03:54, em um total de 1 vez.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Mar 30, 2013 15:33
por e8group » Sáb Mar 30, 2013 15:33
Pensei assim ,
(1)

Conclusões :
(1.a)
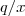
e
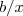
tendem a zero quando
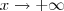
.
(1.b)

está oscilando entre -1 e 1 (limite indefinido ) quando
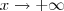
(1.c) (1.a) + (1.b) implica

as parcelas que estão no numerador vão a zero ,isto acontece
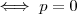
e

.
(2)
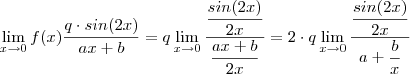
Conclusões :
(2.a) Pelo limite fundamental trigonométrico

.
(2.b) Como

é finito e é igual a 2, temos que

pois caso contrário ,
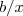
tenderia

e

a zero [pois

](que não é o caso ) .
(3.b) De

concluímos que
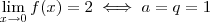
.
Em resumo :

.
Poderia por favor confirma se está certo ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Sáb Mar 30, 2013 16:14
por Douglas16 » Sáb Mar 30, 2013 16:14
Então, eu estava a resolver também, e o que me impedia de finalizar era a condição para o limite de f(x) quando x tende ao infinito, pois mesmo que o valor de p seja constante (ou seja finito) e mesmo que considerasse tal valor igual a zero, ainda assim eu teria a seguinte indeterminação:
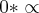
(quando p =0), agora quanto ao restante dos valores das outras constantes eu só não estou com tempo de analisar sua resolução, pois tenho que ir trabalhar agora e se Deus quiser só volto depois de 23:59 hs de hoje, ou seja amanhã por volta das 00:30.
Mas também suspeito que não haja erro na sua resolução, pelo motivo de que a indeterminação pode ser resolvida se este caso ou tipo de situação algébrica permitir.
Mas agradeço se deixar um esclarecimento para o meu erro em relação a definição da indeterminação se caso ele estiver errado ou se estiver correto também agradeço o seu comentário.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Douglas16 » Dom Mar 31, 2013 03:33
por Douglas16 » Dom Mar 31, 2013 03:33
voltei.
Quanto a indeterminação, por se tratar de uma expressão em construção, eu posso admitir o valor de p=0, mas quanto aos valores de a e q, eu posso admitir tanto a=q=2 ou a=q=1.
Se eu estiver errado me corrija.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 31, 2013 09:59
por e8group » Dom Mar 31, 2013 09:59
Sim , e ainda podemos generalizar ,tomar
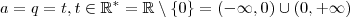
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Condições
 por roninhasmr » Seg Nov 13, 2017 14:24
por roninhasmr » Seg Nov 13, 2017 14:24
- 0 Respostas
- 2130 Exibições
- Última mensagem por roninhasmr

Seg Nov 13, 2017 14:24
Lógica
-
- Classificar condições
 por roninhasmr » Seg Nov 13, 2017 14:31
por roninhasmr » Seg Nov 13, 2017 14:31
- 0 Respostas
- 2346 Exibições
- Última mensagem por roninhasmr

Seg Nov 13, 2017 14:31
Lógica
-
- [Parte financiada?] Condições de venda de uma casa
por pontodigital » Ter Jun 19, 2012 01:20
- 1 Respostas
- 1892 Exibições
- Última mensagem por Fabiano Vieira

Ter Jun 26, 2012 20:47
Matemática Financeira
-
- Como fazer uma função com essas condições
por Arthur_Bulcao » Sex Jun 29, 2012 03:42
- 4 Respostas
- 3150 Exibições
- Última mensagem por LuizAquino

Dom Jul 01, 2012 11:57
Funções
-
- Quantos P primos existe para N natural nessas condições?
por BrenoNaval » Sex Abr 11, 2014 12:05
- 1 Respostas
- 1964 Exibições
- Última mensagem por Mattioli

Sex Jun 06, 2014 00:25
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
,  ,
,  e
e 
 tal que
tal que 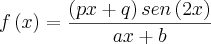 satisfaça
satisfaça 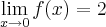 e
e 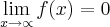 .
.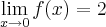 portanto
portanto  e;
e;
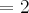 , portanto
, portanto  , portanto
, portanto 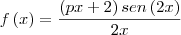 e;
e; , só sei que devo eliminar esta indeterminação, só não sei como.
, só sei que devo eliminar esta indeterminação, só não sei como.
 ,
,  ,
,  e
e 
 tal que
tal que 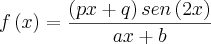 satisfaça
satisfaça 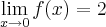 e
e 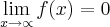 .
.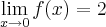 portanto
portanto  e;
e;
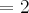 , portanto
, portanto  , portanto
, portanto 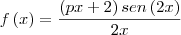 e;
e; , só sei que devo eliminar esta indeterminação, só não sei como.
, só sei que devo eliminar esta indeterminação, só não sei como.

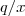 e
e 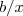 tendem a zero quando
tendem a zero quando 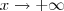 .
.  está oscilando entre -1 e 1 (limite indefinido ) quando
está oscilando entre -1 e 1 (limite indefinido ) quando 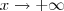
 as parcelas que estão no numerador vão a zero ,isto acontece
as parcelas que estão no numerador vão a zero ,isto acontece 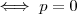 e
e  .
. 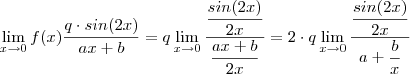
 .
.  é finito e é igual a 2, temos que
é finito e é igual a 2, temos que  pois caso contrário ,
pois caso contrário , 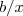 tenderia
tenderia  e
e  a zero [pois
a zero [pois  ](que não é o caso ) .
](que não é o caso ) .  concluímos que
concluímos que 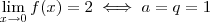 .
.  .
.
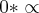 (quando p =0), agora quanto ao restante dos valores das outras constantes eu só não estou com tempo de analisar sua resolução, pois tenho que ir trabalhar agora e se Deus quiser só volto depois de 23:59 hs de hoje, ou seja amanhã por volta das 00:30.
(quando p =0), agora quanto ao restante dos valores das outras constantes eu só não estou com tempo de analisar sua resolução, pois tenho que ir trabalhar agora e se Deus quiser só volto depois de 23:59 hs de hoje, ou seja amanhã por volta das 00:30.

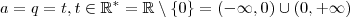 .
.