-tentei resolver a questão:
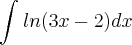
-Consegui, usando substituição para chamar "3x-2" de W. E somente depois aplicar a fórmula da integral por partes. Porque para mim assim fica mais fácil de entender.
- Até aí, tudo bem. O problema foi quando eu tentei resolver o exercício semelhante:
Dúvida:
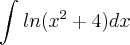
- Aqui, se eu chamo
 de K, por exemplo, para poder usar a substituição. Desse jeito eu chamo "u" de "
de K, por exemplo, para poder usar a substituição. Desse jeito eu chamo "u" de " " e "dv" de "
" e "dv" de "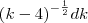 " Mas não dá certo!
" Mas não dá certo! 
- Eu sempre chego em algo parecido com:
![\frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right) \frac{1}{2}.\left(ln(k).arcsen\left(\frac{2}{\sqrt[]{k}}\right)-\int_{}^{}arcsen\left(\frac{2}{\sqrt[]{k}}\right)dk \right)](/latexrender/pictures/cf4d5c1f673aac5a6b192656d1743349.png)
E, se é equivalente, eu não faço a menor idéia de como chegar na resposta do gabarito:
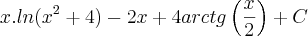
POR FAVOR GALERA. TEM COMO RESOLVE-LO USANDO SUBSTITUIÇÃO?
Att. Matheus L. Oliveira



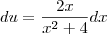


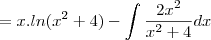

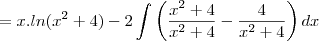


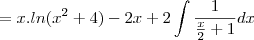

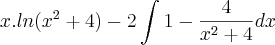
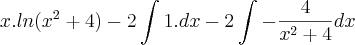
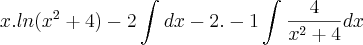

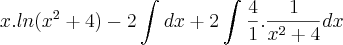
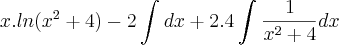








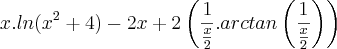
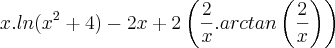



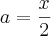








![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)