 por marcosmuscul » Qui Mar 28, 2013 17:23
por marcosmuscul » Qui Mar 28, 2013 17:23
amigos:
a expressão é esta:
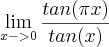
resolvi de dois modos:
modo 1:
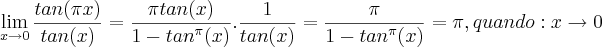
modo 2:
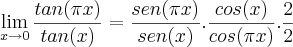
fazendo uso desta propriedade trigonométrica:
http://www.algosobre.com.br/matematica/trigonometria-multiplicacao-e-divisao-de-arcos.htmlaltero a expressão por uma similar:
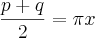
e
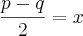
...............resolvendo............
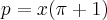
e
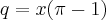
___________________________________________________
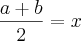
e
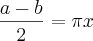
.............resolvendo.............
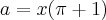
e
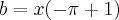
___________________________________________________
a expressão fica então assim:
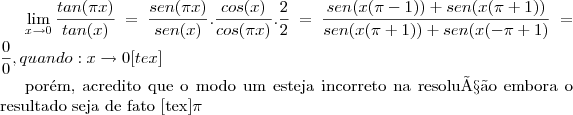
.
alguém poderia me ajudar a encontrar o valor

como resposta?
grato por sua nobreza em ler o tópico.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por marcosmuscul » Qui Mar 28, 2013 18:00
por marcosmuscul » Qui Mar 28, 2013 18:00
amigos. acho que consegui.
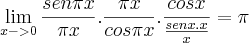
MAs mesmo, assim:
o modo 1 e/ou modo 2 estaria incorreto?
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Qui Mar 28, 2013 18:33
por e8group » Qui Mar 28, 2013 18:33
Poderia por favor mostrar como obteu aquelas relações que você impôs ser igual ao limite no primeiro membro no modo 1 .
Observação : a notação
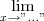
deve ser sempre acompanhada ao lado da expressão a até o limite ser calculado .
Como sugestão ,mostre primeiro que
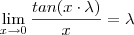
para qualquer

real .Com base neste resultado, conclua que
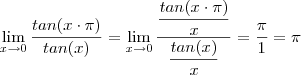
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marcosmuscul » Qui Mar 28, 2013 19:28
por marcosmuscul » Qui Mar 28, 2013 19:28
como eu disse antes, eu tenho certeza que o modo 1 está errado. o resultado foi apenas coincidencia:
já provei o que vc pediu antes do seu post.
aliás, todos sabem a fórmula para tan(2x). Existe alguma formula geral para tan(nx), tal que n>=2 ?
valeu amigo pela ajuda.
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Qui Mar 28, 2013 20:19
por e8group » Qui Mar 28, 2013 20:19
A fórmula para
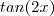
pode ser obtida por soma de ângulos ,sendo
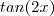
o quociente de
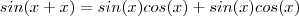
por
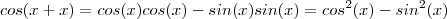
,daí surgi a fórmula que você citou .Mas , para
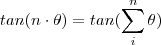
não é tão simples como para
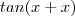
.Veja o seguinte link :
http://en.wikipedia.org/wiki/List_of_tr ... identities , em especial "tangent of sums " .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função implícita]mera coincidência no resultado?
por marcosmuscul » Qua Abr 03, 2013 20:30
- 1 Respostas
- 1413 Exibições
- Última mensagem por Russman

Qua Abr 03, 2013 22:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite]por que houve divergência no resultado?
por marcosmuscul » Qui Mar 28, 2013 19:48
- 1 Respostas
- 1548 Exibições
- Última mensagem por e8group

Qui Mar 28, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Dúvida sobre o resultado de um limite
por Paulo Souza » Dom Ago 25, 2013 20:57
- 0 Respostas
- 1839 Exibições
- Última mensagem por Paulo Souza

Dom Ago 25, 2013 20:57
Cálculo: Limites, Derivadas e Integrais
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3206 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 01:18
Progressões
-
- Confirmação de resultado
por Fabiim » Seg Mai 09, 2011 22:19
- 2 Respostas
- 2904 Exibições
- Última mensagem por Fabiim

Qua Mai 11, 2011 20:49
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
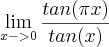
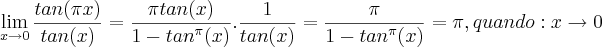
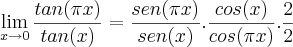
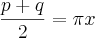 e
e 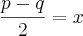
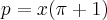 e
e 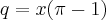
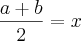 e
e 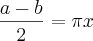
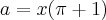 e
e 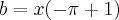
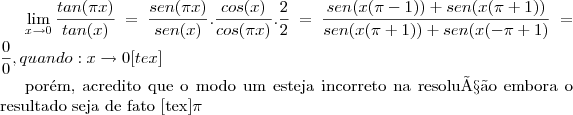 .
. como resposta?
como resposta?

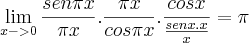
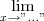 deve ser sempre acompanhada ao lado da expressão a até o limite ser calculado .
deve ser sempre acompanhada ao lado da expressão a até o limite ser calculado . 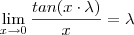 para qualquer
para qualquer  real .Com base neste resultado, conclua que
real .Com base neste resultado, conclua que 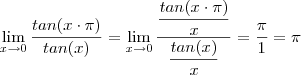 .
.
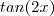 pode ser obtida por soma de ângulos ,sendo
pode ser obtida por soma de ângulos ,sendo 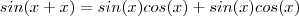 por
por 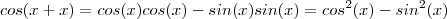 ,daí surgi a fórmula que você citou .Mas , para
,daí surgi a fórmula que você citou .Mas , para 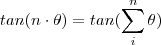 não é tão simples como para
não é tão simples como para 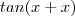 .Veja o seguinte link :
.Veja o seguinte link : 

 , avisa que eu resolvo.
, avisa que eu resolvo.

