




 , onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx = 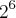 = 64, e n4 =
= 64, e n4 = 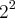 = 4. Sabendo que o vazio pertence a todo conjunto!
= 4. Sabendo que o vazio pertence a todo conjunto!
timoteo escreveu:Correto,
olhando agora vejo que ele considera n4 é subconjunto de x e o numero de elementos de n4 realmente não é maior que o número de elementos de nx.
Para calcular o número de elementos usa-se a fórmula:, onde n representa o número de elementos do conjunto. Sendo assim, temos: nx =
= 64, e n4 =
= 4. Sabendo que o vazio pertence a todo conjunto!
Espero ter ajudado!
 . Chegando-se a 64 subconjuntos. Estes 64 subconjuntos
. Chegando-se a 64 subconjuntos. Estes 64 subconjuntos

timoteo escreveu:Obrigado pelo elogio. Espero que você não esteja me estudando para alguma tese de psicologia. Rsrsrsrs...
Todos aqui são bons!
Bem, em relação a seu questionamento, sim, vocês está correta. Para mais conhecimento você deveria ver propriedades do conjunto da partes!
Espero ter ajudado!

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)