 por Amorais » Dom Mar 24, 2013 20:34
por Amorais » Dom Mar 24, 2013 20:34
Tenho essas questões que estou tentando resolver
já tentei usar integração por partes e por substituição.
Alguém pode me dá uma dica ?
A resposta dela já vem logo abaixo

-
Amorais
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 24, 2013 20:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Mecânica.
- Andamento: cursando
 por nakagumahissao » Dom Mar 24, 2013 20:58
por nakagumahissao » Dom Mar 24, 2013 20:58
Tente fazer:
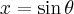
Mais para a frente, use:
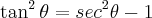
Creio que isto deve ajudar.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por LuizAquino » Dom Mar 24, 2013 21:16
por LuizAquino » Dom Mar 24, 2013 21:16
Amorais escreveu:Tenho essas questões que estou tentando resolver
já tentei usar integração por partes e por substituição.
Alguém pode me dá uma dica ?
A resposta dela já vem logo abaixo
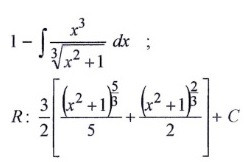
- anexo.jpg (8.51 KiB) Exibido 23753 vezes
Usando as substituições
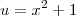
e

, temos que:
![\int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \int \dfrac{x^2\cdot x}{\sqrt[3]{x^2 + 1}}\, dx \int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \int \dfrac{x^2\cdot x}{\sqrt[3]{x^2 + 1}}\, dx](/latexrender/pictures/7c2e592b240baf10af2021c948a44501.png)
![= \dfrac{1}{2}\int \dfrac{u - 1}{\sqrt[3]{u}}\, du = \dfrac{1}{2}\int \dfrac{u - 1}{\sqrt[3]{u}}\, du](/latexrender/pictures/56413dcff0e32a0f4b5e82254bddb980.png)
![= \dfrac{1}{2}\int \dfrac{u}{\sqrt[3]{u}}\, du - \dfrac{1}{2} \int \dfrac{1}{\sqrt[3]{u}}\,du = \dfrac{1}{2}\int \dfrac{u}{\sqrt[3]{u}}\, du - \dfrac{1}{2} \int \dfrac{1}{\sqrt[3]{u}}\,du](/latexrender/pictures/a6a4187d24558a4db47136282eaa140d.png)
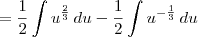
Agora tente concluir o exercício a partir daí.
Observação 1O gabarito apresentado contém um erro. Na verdade, o correto será:
![\int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \dfrac{3}{2} \left[\dfrac{\left(x^2 + 1\right)^{\frac{5}{3}}}{5} - \dfrac{\left(x^2 + 1\right)^{\frac{2}{3}}}{2}\right] + C \int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \dfrac{3}{2} \left[\dfrac{\left(x^2 + 1\right)^{\frac{5}{3}}}{5} - \dfrac{\left(x^2 + 1\right)^{\frac{2}{3}}}{2}\right] + C](/latexrender/pictures/a3f062398fc99aa58258dbbfb8a0c038.png) Observação 2
Observação 2Por favor, antes de postar um tópico leia as
Regras deste Fórum. Em especial, vide a regra 3.
Nós recomendamos também que você leia o tópico abaixo:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Amorais » Dom Mar 24, 2013 21:37
por Amorais » Dom Mar 24, 2013 21:37
Obrigado amigos LuizAquino, nakagumahissao.
Me decupem pelo erro na postagem.
-
Amorais
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 24, 2013 20:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Mecânica.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- qual é a dica
por darlan2009 » Qua Ago 29, 2012 10:23
- 2 Respostas
- 23361 Exibições
- Última mensagem por Daisy221

Qua Mai 31, 2017 05:21
Análise Combinatória
-
- Dica de livro - Trigonometria
por renanrdaros » Dom Mar 27, 2011 04:06
- 4 Respostas
- 22119 Exibições
- Última mensagem por renanrdaros

Qui Mar 31, 2011 11:40
Trigonometria
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3445 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- [DICA] Livro de Matemática Ensino Fundamental
por invader_zim » Seg Fev 11, 2013 14:54
- 9 Respostas
- 9620 Exibições
- Última mensagem por alex_08

Ter Fev 12, 2013 18:01
Álgebra Elementar
-
- [Funções injetoras/sobrejetoras] Dica para determinar
por vitor_jo » Qua Jan 21, 2015 05:56
- 2 Respostas
- 5536 Exibições
- Última mensagem por vitor_jo

Qua Jan 21, 2015 16:47
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




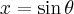
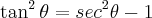

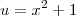 e
e  , temos que:
, temos que:![\int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \int \dfrac{x^2\cdot x}{\sqrt[3]{x^2 + 1}}\, dx \int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \int \dfrac{x^2\cdot x}{\sqrt[3]{x^2 + 1}}\, dx](/latexrender/pictures/7c2e592b240baf10af2021c948a44501.png)
![= \dfrac{1}{2}\int \dfrac{u - 1}{\sqrt[3]{u}}\, du = \dfrac{1}{2}\int \dfrac{u - 1}{\sqrt[3]{u}}\, du](/latexrender/pictures/56413dcff0e32a0f4b5e82254bddb980.png)
![= \dfrac{1}{2}\int \dfrac{u}{\sqrt[3]{u}}\, du - \dfrac{1}{2} \int \dfrac{1}{\sqrt[3]{u}}\,du = \dfrac{1}{2}\int \dfrac{u}{\sqrt[3]{u}}\, du - \dfrac{1}{2} \int \dfrac{1}{\sqrt[3]{u}}\,du](/latexrender/pictures/a6a4187d24558a4db47136282eaa140d.png)
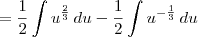
![\int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \dfrac{3}{2} \left[\dfrac{\left(x^2 + 1\right)^{\frac{5}{3}}}{5} - \dfrac{\left(x^2 + 1\right)^{\frac{2}{3}}}{2}\right] + C \int \dfrac{x^3}{\sqrt[3]{x^2 + 1}}\, dx = \dfrac{3}{2} \left[\dfrac{\left(x^2 + 1\right)^{\frac{5}{3}}}{5} - \dfrac{\left(x^2 + 1\right)^{\frac{2}{3}}}{2}\right] + C](/latexrender/pictures/a3f062398fc99aa58258dbbfb8a0c038.png)


