 por Ge_dutra » Qui Mar 21, 2013 20:58
por Ge_dutra » Qui Mar 21, 2013 20:58
Seja f:

tal que f'(x)=f(x). Encontrar (

(x)
Não consegui chegar a um raciocínio muito coerente, tentei várias vezes e não está batendo com o gabarito (

, x>0)
Podem ajudar?
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sex Mar 22, 2013 09:33
por e8group » Sex Mar 22, 2013 09:33
Presumo que a hipótese seja
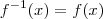
e ainda

.
Solução :
Como

,existe uma função

invertível,

tal que

,sendo assim ,
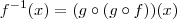
(Por quê ? ) . Mas ,
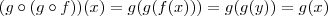
, daí
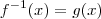
,observe que

pois
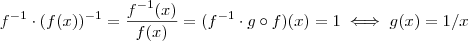
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ge_dutra » Sex Mar 22, 2013 10:43
por Ge_dutra » Sex Mar 22, 2013 10:43
Confesso que não entendi a sua resolução. A menos que o exercício esteja errado, o domínio de f não exclui o zero, e nada fala sobre

(x) ser igual a f(x), e sim que a derivada de f(x) é igual a f(x).
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sex Mar 22, 2013 11:52
por e8group » Sex Mar 22, 2013 11:52
Desculpe o equivoco ,sendo

observe que
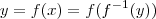
,derivando ambos membros com respeito a

,

.
Observações :
a)
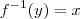
b)

Por a ) e b) obtemos :

que devido a hipótese

resulta
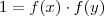
,ou seja ,

,logo ,

.
Não sei se está certo ,se sim ,há uma contradição ,pois se

e
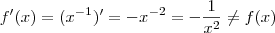
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ge_dutra » Sex Mar 22, 2013 12:11
por Ge_dutra » Sex Mar 22, 2013 12:11
Achei essa questão um pouco confusa. Vou tentar conseguir a resolução dela hoje e postarei aqui.
De qualquer forma obrigada pela atenção e ajuda.
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Ge_dutra » Sex Mar 22, 2013 23:18
por Ge_dutra » Sex Mar 22, 2013 23:18
Santhiago, a resolução é mais simples do que aparenta
Sendo

E f'(x) = f(x), temos que
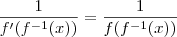
Como

,

, x>0
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Sáb Mar 23, 2013 09:43
por e8group » Sáb Mar 23, 2013 09:43
OK ! Boa resolução ,obrigado por compartilhar . Só uma dúvida, a resposta final não deveria ser
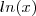
? Pois,
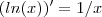
e pelo enunciado pede-se para encontrar

,a menos que seja para encontrar

(que neste caso a resposta é apenas

),mas para encontrar
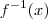
,precisará
integrar ambos membros com respeito a

,caso você não conheça este conceito ,acredito que realmente o objetivo proposto pelo enunciado seja encontrar

e não

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Ge_dutra » Sáb Mar 23, 2013 16:02
por Ge_dutra » Sáb Mar 23, 2013 16:02
Acabo de perceber que fiz uma pequena confusão. Realmente o enunciado pedia para encontrar
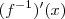
.Erro meu, desculpe!
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3397 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- O que é função inversa
por irineu junior » Sex Mar 12, 2010 20:57
- 2 Respostas
- 2642 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 16:28
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7729 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1185 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2209 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tal que f'(x)=f(x). Encontrar (
tal que f'(x)=f(x). Encontrar ( (x)
(x)  , x>0)
, x>0)
 tal que f'(x)=f(x). Encontrar (
tal que f'(x)=f(x). Encontrar ( (x)
(x)  , x>0)
, x>0)
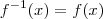 e ainda
e ainda  .
. ,existe uma função
,existe uma função  invertível,
invertível,  tal que
tal que  ,sendo assim ,
,sendo assim , 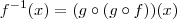 (Por quê ? ) . Mas ,
(Por quê ? ) . Mas , 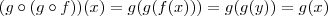 , daí
, daí 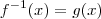 ,observe que
,observe que  pois
pois 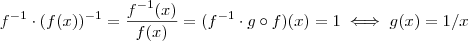 .
.
 (x) ser igual a f(x), e sim que a derivada de f(x) é igual a f(x).
(x) ser igual a f(x), e sim que a derivada de f(x) é igual a f(x).
 observe que
observe que 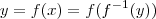 ,derivando ambos membros com respeito a
,derivando ambos membros com respeito a  ,
,  .
. 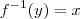

 que devido a hipótese
que devido a hipótese  resulta
resulta 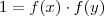 ,ou seja ,
,ou seja ,  ,logo ,
,logo , .
. e
e 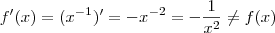 .
.


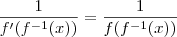
 ,
,  , x>0
, x>0
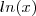 ? Pois,
? Pois, 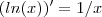 e pelo enunciado pede-se para encontrar
e pelo enunciado pede-se para encontrar  ,a menos que seja para encontrar
,a menos que seja para encontrar  (que neste caso a resposta é apenas
(que neste caso a resposta é apenas  ),mas para encontrar
),mas para encontrar 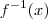 ,precisará integrar ambos membros com respeito a
,precisará integrar ambos membros com respeito a  ,caso você não conheça este conceito ,acredito que realmente o objetivo proposto pelo enunciado seja encontrar
,caso você não conheça este conceito ,acredito que realmente o objetivo proposto pelo enunciado seja encontrar  e não
e não  .
.
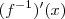 .Erro meu, desculpe!
.Erro meu, desculpe!


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.