Olá, não consigo resolver esse problema:
Ação global contra petróleo caro
A Agência Internacional de Energia (AIE), formada por
28 países, anunciou ontem a liberação de 60 milhões
de barris de petróleo de reservas estratégicas [...].
Os EUA vão entrar com metade do volume, [...] a
Europa irá colaborar com , e o restante virá de
Austrália, Japão, Coreia e Nova Zelândia.
O Globo, Rio de Janeiro, p. 17. 24 jun. 2011. Adaptado.
Suponha que os países asiáticos (Japão e Coreia) contribuam
juntos com 1,8 milhão de barris a mais do que
a contribuição total dos países da Oceania (Austrália e
Nova Zelândia).
Desse modo, quantos milhões de barris serão disponibilizados
pelos países asiáticos?
(A) 5,2
(B) 5,6
(C) 6,9
(D) 7,4
(E) 8,2
A resposta é C.
Pensei assim: 60 milhões, metade fica sob responsabilidade dos EUA (30 milhoes);
30 * 3/10 = 9 milhões da Europa
sobra 21 milhões para dividir para 4 países = 5,25 para cada país.
10,25 é a soma dos dois países mencionados, acrescido 1,8 milhões de barris que tais países irão pagar a mais que os outros dois: 8,7 - errado.
Alguém me ajuda, por favor?
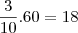
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.