 Tenho essa integral, fiz a integração por partes duas vezes e cheguei a:
Tenho essa integral, fiz a integração por partes duas vezes e cheguei a:  só que segundo uma resolução de um colega, essa parte que eu cheguei é igual a:
só que segundo uma resolução de um colega, essa parte que eu cheguei é igual a:  seguindo com com pi/3 e zero, e dai a resposta vai dar 3/2.1/8+3/8= 9/16
seguindo com com pi/3 e zero, e dai a resposta vai dar 3/2.1/8+3/8= 9/16Qual relação existe entre:
 e
e 
será a continuação? por qual motivo? o que meu colega fez e não estou conseguindo compreender?
Desde já agradeço a disposição de vocês, obrigado!


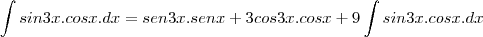
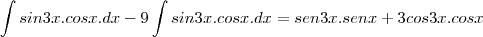
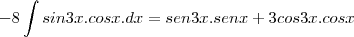
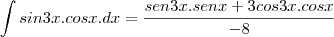


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)