Mas não sei como na penúltima equação a expressão: fatorial de b, sobre, o fatorial de n, é igual a:
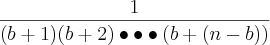
E também como provar a afirmação: "E o resultado segue, pois como é fácil ver 2<e<3"; não encontro a prova!!!???
O resto entendi, ok?

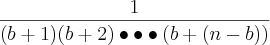

 e ambos são naturais .Certo ?
e ambos são naturais .Certo ?  natural tal que
natural tal que  (Não é verdade ? )
(Não é verdade ? )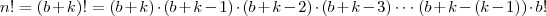 .
.  , segue que
, segue que ![n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b! n! = (b+[n -b])\cdot (b+[n -b] -1)\cdot (b+[n -b]-2)\cdot (b+[n -b]-3) \cdots (b +1) ) \cdot b!](/latexrender/pictures/21393c327fa4a29315160b57ca55c2d7.png) que simplificando ficamos apenas com ,
que simplificando ficamos apenas com ,  .
. 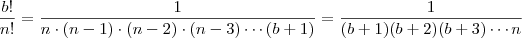 .
.
 (é irracional)
(é irracional)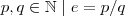
 por
por 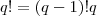 ,temos
,temos  .
. 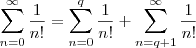 ,então :
,então : 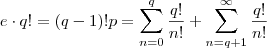 .
.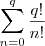 e
e 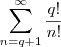 também são naturais .
também são naturais . 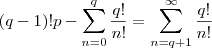
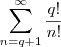 não é natural ,está concluída a prova .
não é natural ,está concluída a prova . 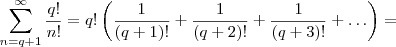

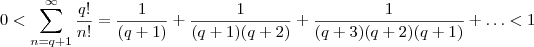
 .
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

