 por Danilo » Sáb Mar 09, 2013 12:16
por Danilo » Sáb Mar 09, 2013 12:16
Eu estava resolvendo um exercício de indução mas não consegui deixar a resposta como na do livro.
Cheguei a


e quero chegar a (mas não sei como)
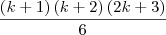
Grato a quem puder ajudar !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Mar 09, 2013 13:16
por e8group » Sáb Mar 09, 2013 13:16
Boa tarde . Deixando

em evidência ,temos no numerador
![(k+1)[k(2k+1) +6(k+1)] (k+1)[k(2k+1) +6(k+1)]](/latexrender/pictures/d8ed976015e7602de6e29edbc8b4b636.png)
.
De
![2k+1 = [2k+3] +(-2) 2k+1 = [2k+3] +(-2)](/latexrender/pictures/34b1be84642392b1b59361281a48e677.png)
, obtemos
![k(2k+1) = k([2k+3] +(-2)) k(2k+1) = k([2k+3] +(-2))](/latexrender/pictures/0715b66a2c686686190c6733330546e7.png)
e ainda por distributividade resulta ,
![[2k+3]k - 2k [2k+3]k - 2k](/latexrender/pictures/6580010d3b8fd05df1884c80186805e1.png)
; logo ,
![k(2k+1) +6(k+1) = [2k+3]k - 2k + 6(k+1) = [2k+3]k +(6k +(-2k) ) + 6 = [2k+3]k + 4k +6 = [2k+3]k + 2[2k+3] = [2k+3][k+2]= k(2k+1) +6(k+1) = [2k+3]k - 2k + 6(k+1) = [2k+3]k +(6k +(-2k) ) + 6 = [2k+3]k + 4k +6 = [2k+3]k + 2[2k+3] = [2k+3][k+2]=](/latexrender/pictures/a4434813982a2e7b1a390db98b570a25.png)
e portanto ,
![(k+1)[k(2k+1) +6(k+1)] = [k+1][2k+3][k+2] (k+1)[k(2k+1) +6(k+1)] = [k+1][2k+3][k+2]](/latexrender/pictures/b3bf5f9b9e55c9ad7bcbc492ed73a2c0.png)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na Fatoração
por runksoneck » Sáb Fev 19, 2011 18:30
- 2 Respostas
- 4360 Exibições
- Última mensagem por runksoneck

Ter Fev 22, 2011 09:57
Pedidos
-
- dúvida fatoração
por Andrewo » Ter Mar 13, 2012 16:51
- 5 Respostas
- 2809 Exibições
- Última mensagem por LuizAquino

Qua Mar 28, 2012 17:19
Álgebra Elementar
-
- Fatoração - dúvida
por laura_biscaro » Sex Mar 15, 2013 01:06
- 3 Respostas
- 2079 Exibições
- Última mensagem por DanielFerreira

Dom Mar 17, 2013 18:57
Álgebra Elementar
-
- [Fatoração] Duvida.
por replay » Sex Mar 15, 2013 12:43
- 7 Respostas
- 4257 Exibições
- Última mensagem por timoteo

Qui Mar 21, 2013 12:23
Álgebra Elementar
-
- [Fatoração] Dúvida em exercício
por Antonio Unwisser » Sáb Ago 30, 2014 21:36
- 3 Respostas
- 2284 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 21:22
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


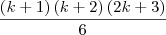



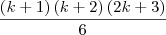

 em evidência ,temos no numerador
em evidência ,temos no numerador ![(k+1)[k(2k+1) +6(k+1)] (k+1)[k(2k+1) +6(k+1)]](/latexrender/pictures/d8ed976015e7602de6e29edbc8b4b636.png) .
.![2k+1 = [2k+3] +(-2) 2k+1 = [2k+3] +(-2)](/latexrender/pictures/34b1be84642392b1b59361281a48e677.png) , obtemos
, obtemos ![k(2k+1) = k([2k+3] +(-2)) k(2k+1) = k([2k+3] +(-2))](/latexrender/pictures/0715b66a2c686686190c6733330546e7.png) e ainda por distributividade resulta ,
e ainda por distributividade resulta ,![[2k+3]k - 2k [2k+3]k - 2k](/latexrender/pictures/6580010d3b8fd05df1884c80186805e1.png) ; logo ,
; logo , ![k(2k+1) +6(k+1) = [2k+3]k - 2k + 6(k+1) = [2k+3]k +(6k +(-2k) ) + 6 = [2k+3]k + 4k +6 = [2k+3]k + 2[2k+3] = [2k+3][k+2]= k(2k+1) +6(k+1) = [2k+3]k - 2k + 6(k+1) = [2k+3]k +(6k +(-2k) ) + 6 = [2k+3]k + 4k +6 = [2k+3]k + 2[2k+3] = [2k+3][k+2]=](/latexrender/pictures/a4434813982a2e7b1a390db98b570a25.png)
![(k+1)[k(2k+1) +6(k+1)] = [k+1][2k+3][k+2] (k+1)[k(2k+1) +6(k+1)] = [k+1][2k+3][k+2]](/latexrender/pictures/b3bf5f9b9e55c9ad7bcbc492ed73a2c0.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)