 por klueger » Qua Mar 06, 2013 23:03
por klueger » Qua Mar 06, 2013 23:03
Não tenho noção... a unica dica que deram é usar o
segundo caso de Substituição que seria

*Uma barra carregada de comprimento L produz um campo elétrico no ponto P(a,b) fora da barra, para calcular o campo elétrico, usamos a integral abaixo.

*em que
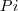
é a densidade de carga por unidade de comprimento da barra e
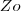
é a permissividade do vácuo. Usando substituição trigonométrica,
calcule a integral para determinar uma expressão para o campo elétrico E(P) !!
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 00:37
por Russman » Qui Mar 07, 2013 00:37
Esse ponto P esta situado onde? Não tem alguma figura esse problema?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por klueger » Qui Mar 07, 2013 00:42
por klueger » Qui Mar 07, 2013 00:42
.
Editado pela última vez por
klueger em Qui Mar 07, 2013 00:44, em um total de 1 vez.
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por klueger » Qui Mar 07, 2013 00:44
por klueger » Qui Mar 07, 2013 00:44
Russman escreveu:Esse ponto P esta situado onde? Não tem alguma figura esse problema?
Não... só pede a integral para ter uma expressão desse campo elétrico E(P)
-
klueger
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Fev 03, 2013 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Mar 07, 2013 01:45
por Russman » Qui Mar 07, 2013 01:45
Você precisa decompor o campo elétrico em componentes e integra-las usando o ângulo formado entre a linha perpendicular a barra, que a liga com o ponto P, e uma imaginária que ligue um diferencial de comprimento da mesma como variável de integração.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3756 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao trigonometrica 3
por beel » Dom Nov 27, 2011 18:24
- 3 Respostas
- 2899 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:44
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2061 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1487 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
-
- integral substituição trigonométrica
por samysoares » Dom Mai 26, 2013 17:13
- 1 Respostas
- 1355 Exibições
- Última mensagem por e8group

Dom Mai 26, 2013 19:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


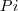 é a densidade de carga por unidade de comprimento da barra e
é a densidade de carga por unidade de comprimento da barra e 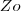 é a permissividade do vácuo. Usando substituição trigonométrica, calcule a integral para determinar uma expressão para o campo elétrico E(P) !!
é a permissividade do vácuo. Usando substituição trigonométrica, calcule a integral para determinar uma expressão para o campo elétrico E(P) !!




 , avisa que eu resolvo.
, avisa que eu resolvo.

